Fun with zeta functions

February 4, 2009

In mpmath-trunk there is now an implementation of the Riemann-Siegel Z function as well as the related Riemann-Siegel theta function. There is also a function for computing Gram points.

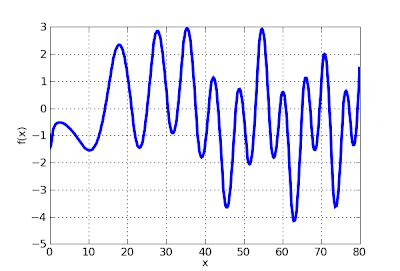
A picture is worth a thousand words. The Z function is a kind of real-valued version of the Riemann zeta function on the critical strip (compare to this previous plot):

>>> from mpmath import *
>>> plot(siegelz, [0,80])

The implementation is entirely generic, so it works in the complex numbers:

>>> cplot(siegelz, points=50000)

>>> cplot(siegelz, [-25,25], [-25,25], points=50000)

Gram points are useful for locating zeros of the zeta/Z functions. Huge Gram points themselves are easily located:

>>> mp.dps = 50
>>> print grampoint(10**10)
3293531632.7283354545611526800803306343201329980271

Unfortunately, evaluation of the Riemann zeta or Riemann-Siegel Z functions is not feasible for such large inputs with the present zeta function implementation in mpmath. Lowering expectations a bit, one can still compute some fairly large zeros:

>>> g1 = grampoint(1000)
>>> g2 = grampoint(1001)
>>> r = findroot(siegelz, [g1, g2], solver='illinois')
>>> print r
1421.8505671870486539107068075509847506037846486061
>>> print g1 < r < g2
True
>>> nprint(siegelz(r))
-1.30567e-51

(I chose the Illinois solver here because it combines bracketing with the fast convergence of the secant method.)

A plot of the initial couple of Gram points:

>>> mp.dps = 15
>>> plot(lambda x: grampoint(floor(x)), [0, 30])

The following visualization of Gram points is perhaps more illustrative. It is usually the case that the Gram points and sign changes (i.e. zeros) of Z alternate with each other:


>>> gs = [grampoint(n) for n in range(25)]
>>> def marker(x):
...     for g in gs:
...         if abs(g-x) < 0.2:
...             return 1
...     return 0
...
>>> plot([siegelz, marker], [0,50])

Put another way, it is usually the case that (-1)ⁿ Z(g_n) is positive (this is Gram’s law):

>>> (-1)**10 * siegelz(grampoint(10)) > 0
True
>>> (-1)**11 * siegelz(grampoint(11)) > 0
True
>>> (-1)**12 * siegelz(grampoint(12)) > 0
True

The first exception occurs at n = 126 (more exceptions are listed in OEIS A114856). The Gram point is very close to a root:

>>> (-1)**126 * siegelz(grampoint(126)) > 0
False
>>> mp.dps = 50
>>> print grampoint(126)
282.4547208234621746108397940690599354048302480008
>>> print findroot(siegelz, grampoint(126))
282.46511476505209623302720118650102420550683628035
>>> print siegelz(grampoint(126))
-0.02762949885719993669875120344077657187547768743854

Now, it takes only a few lines of code to enumerate exceptions to Gram’s law, up to say n = 2000:


>>> mp.dps = 10
>>> for k in range(2000):
...     g = grampoint(k)
...     s = siegelz(g)
...     if (-1)**k * s < 0:
...         print k, g, s
...
126 282.4547208 -0.02762949482
134 295.583907 -0.01690039157
195 391.4482021 0.0232894207
211 415.60146 0.3828895679
232 446.8057559 -0.1410432574
254 478.9568293 -0.0600779492
288 527.6973416 -0.6654588176
367 637.320354 0.1579920088
377 650.8910448 0.8376010676
379 653.5978317 0.217352745
397 677.8523216 0.1342801302
400 681.8765522 -0.06717029681
461 762.6678783 0.1525747623
507 822.4194896 0.7419389942
518 836.5739092 -0.3982959071
529 850.6795334 0.1756176097
567 899.0502587 0.8296209263
578 912.9534756 -0.3537611108
595 934.3572317 0.121967239
618 963.1605748 -0.04025206217
626 973.1388241 -0.1578260824
637 986.8259207 0.2852904149
654 1007.905352 -0.5547383392
668 1025.199826 -0.2608153866
692 1054.715528 -0.07836895313
694 1057.167832 -0.1696327251
703 1068.189532 1.004550445
715 1082.850818 0.1608682601
728 1098.690513 -0.6875362205
766 1144.741881 -0.1678183794
777 1158.005614 9.646277741e-3
793 1177.246581 0.7011668936
795 1179.647457 0.3577242914
807 1194.033228 0.7072513907
819 1208.386043 0.2285739236
848 1242.939633 -0.6161899199
857 1253.626041 0.2131228775
869 1267.84791 1.271208219
887 1289.124631 0.1830773844
964 1379.419269 -1.392200147
992 1411.979146 -0.06783933868
995 1415.459427 0.2623456354
1016 1439.777518 -0.9324891715
1028 1453.639612 -0.3106139874
1034 1460.561547 -0.6501820215
1043 1470.933184 0.0987483831
1046 1474.387414 -0.5680195111
1071 1503.115534 0.1530310857
1086 1520.304266 -0.106037306
1094 1529.457103 -0.1839654392
1111 1548.873932 0.02102960258
1113 1551.155349 0.8003510427
1135 1576.211048 0.2276419942
1156 1600.060766 -0.02925581253
1165 1610.262397 8.575848564e-3
1178 1624.977566 -0.2655885013
1207 1657.717899 0.8645603918
1209 1659.971552 0.36625445
1231 1684.725787 0.6156424059
1250 1706.052177 -0.8285966558
1263 1720.616514 0.8288043998
1276 1735.158918 -0.02734148029
1290 1750.795762 -0.1953269334
1294 1755.258868 -0.2675606503
1307 1769.750095 0.5163671897
1319 1783.107961 0.09216880716
1329 1794.225992 0.3012117179
1331 1796.448134 0.1319941485
1342 1808.661254 -0.1258506495
1344 1810.880254 -0.03061304567
1402 1875.026023 -0.5758575812
1430 1905.854681 -1.184795762
1443 1920.138276 1.294805086
1456 1934.403327 -0.03436404474
1485 1966.159589 0.3192688646
1487 1968.346369 0.864509178
1495 1977.089273 0.1463922251
1498 1980.366127 -0.01464596441
1513 1996.736314 0.2570944738
1517 2001.097757 0.8247075447
1532 2017.438527 -0.1691755392
1543 2029.407189 0.1807441973
1545 2031.581995 1.207382688
1600 2091.233527 -0.03995365882
1613 2105.289905 0.4695228803
1620 2112.852035 -0.3058765971
1643 2137.666434 0.8692760726
1646 2140.899441 -0.2679836804
1656 2151.670095 -0.4251702923
1669 2165.658156 0.9247164091
1672 2168.883971 -0.01601726917
1684 2181.779042 -0.1420385576
1702 2201.097281 -1.274939957
1704 2203.241961 -0.2540991172
1722 2222.528116 -0.3804543179
1744 2246.06145 -0.1531821977
1747 2249.267282 1.366292187
1760 2263.150267 -0.7349734815
1773 2277.0188 0.4817831199
1787 2291.938132 0.06919712065
1796 2301.520437 -0.1687993299
1804 2310.032371 -0.687368415
1816 2322.790332 -0.1377354318
1819 2325.977969 0.1645731507
1843 2351.452601 0.01004227096
1850 2358.873909 -0.10089997
1856 2365.231898 -0.1952129943
1863 2372.645911 1.120344703
1876 2386.404453 -0.1397386302
1892 2403.31974 -0.6220070934
1902 2413.881627 -0.367836015
1921 2433.927875 0.01043043105
1933 2446.574386 1.413878285
1935 2448.681071 1.881639813
1953 2467.627613 0.05088637184
1969 2484.448555 0.2965372534
1982 2498.101553 -0.3858252138

(Note: the Z values are not quite accurate to the indicated precision, due to the magnitude of the Gram points. Increasing the precision, one finds siegelz(grampoint(1982)) = -0.385825235416...)

For those interested in this topic, there is a very nice book called “Riemann’s Zeta Function” by H. M. Edwards. There is just as much information to be found on the web, e.g. on the amazing “Numbers, constants and computation” site by Xavier Gourdon and Pascal Sebah.

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor