3D visualization of complex functions with matplotlib

August 9, 2009

Hooray! matplotlib 0.99 is out and it has 3D plotting, finally!

I’ve shown a lot of color plots of complex functions on this blog to demonstrate complex functions in mpmath. These plots are informative, but sometimes a 3D plot (typically of the function’s absolute value) gives a much better view. A big advantage of 3D plots over 2D color plots is that far fewer evaluation points are required for a good high-resolution image, and this helps when visualizing the slower functions in mpmath.

There will probably be a 3D plot function in a future version of mpmath (or two functions; for two-variable real, and complex functions), similar in style to the existing matplotlib wrappers plot and cplot. Until I’ve figured out the details, I’ll share a couple of test plots.

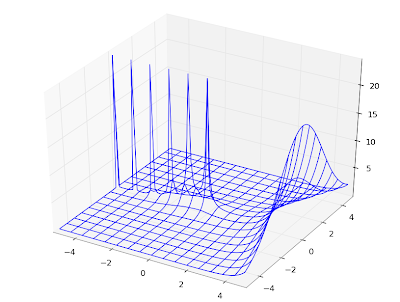
Coulomb wave function of a complex argument, F(6,4,z):

Principal-branch logarithmic gamma function:

Gamma function:

Imaginary part of Lambert W function, 0th branch:

Riemann zeta function in the critical strip:

Those are all wireframe plots. It’s also possible to do surface plots. Using the Riemann zeta function again, a surface plot looks as follows:

Surface + wireframe plot:

None of these is perfect. I’d like to be able to do a surface plot with a widely spaced wireframe mesh to pronounce the geometry, and smooth colored surface between the meshes. This doesn’t seem possible with matplotlib because the surface plot doesn’t do smoothing (even with a stride selected); overlaying a wireframe works decently, but the wireframe doesn’t render with occlusion and this looks bad for some functions. Since the pure wireframe plot is much faster, I think I prefer it for now.

For complex functions, it’d also be nice with a color function separate from the geometry function — then you could plot the phase as color in the same picture.

Color helps for visualizing complicated structure, especially for phase plots. Below, I’ve plotted the phase (actually the sine of the phase, to make it continuous) of a Jacobi theta function θ₃(1+4j/3,q) (restricted to |q| < 0.8, because it gets extremely messy for larger |q|):

The phase of the Barnes G-function:

I could do many more, but that will probably enough for this blog :-)

To reproduce any of these, use the following script with trivial modifications. It’s a straightforward extension of the example scripts in the matplotlib documentation.


from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import pylab
import numpy as np
import mpmath
mpmath.dps = 5

# Use instead of arg for a continuous phase
def arg2(x):
    return mpmath.sin(mpmath.arg(x))

#f = lambda z: abs(mpmath.loggamma(z))
#f = lambda z: arg2(mpmath.exp(z))
#f = lambda z: abs(mpmath.besselj(3,z))
f = lambda z: arg2(mpmath.cos(z))

fig = pylab.figure()
ax = Axes3D(fig)
X = np.arange(-5, 5, 0.125)
Y = np.arange(-5, 5, 0.125)
X, Y = np.meshgrid(X, Y)
xn, yn = X.shape
W = X*0
for xk in range(xn):
    for yk in range(yn):
        try:
            z = complex(X[xk,yk],Y[xk,yk])
            w = float(f(z))
            if w != w:
                raise ValueError
            W[xk,yk] = w
        except (ValueError, TypeError, ZeroDivisionError):
            # can handle special values here
            pass
    print xk, xn

# can comment out one of these
ax.plot_surface(X, Y, W, rstride=1, cstride=1, cmap=cm.jet)
ax.plot_wireframe(X, Y, W, rstride=5, cstride=5)

pylab.show()

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor