fredrikj.net / blog /

Precise computation of roots of unity

February 26, 2013

In various applications, one needs high-precision numerical values of roots of unity, say $e^{\pi i p / q}$ where $p$ and $q$ are integers. A notorious example of this is the Hardy-Ramanujan-Rademacher formula for the partition function
$$p(n) = \sum_{k=1}^{\infty} \left(\sqrt{\frac{3}{k}} \, \frac{4}{24n-1}\right) A_k(n) \; U_k(n)$$
where $U_k(n)$ is a certain hyperbolic function, and where the culprit is the exponential sum
$$A_k(n) = \sum_{h=0}^{k-1} \delta_{\gcd(h,k),1} \exp\left(\pi i \left[s(h,k) - \frac{2hn}{k} \right]\right)$$
in which $s(h,k)$ denotes the Dedekind sum $s(h,k) = \sum_{i=1}^{k-1} \frac{i}{k} \left( \frac{hi}{k} – \left\lfloor \frac{hi}{k} \right\rfloor – \frac{1}{2} \right).$

As I noted in my paper about computing the partition function, there are tricks (using identities by Selberg and Whiteman) which allow one to drastically reduce the amount of roots of unity that need to be evaluated for each $A_k(n)$. But even with this (substantial) improvement implemented, one still needs to evaluate heaps of roots of unity in order to compute $p(n)$ when $n$ is large.

How can we evaluate roots of unity? We may start by noting that the problem is equivalent to computing either the real part $\cos(p\pi/q)$ or the imaginary part $\sin(p\pi/q)$ of a complex exponential, since according to a famous observation by Pythagoras, the other component is just one squaring and a square root away. In fact, even this step is often unnecessary, as in many cases where a complex exponential appears in a formula, it turns out that we can eliminate the real or imaginary part entirely using symmetries. The exponential sums in Rademacher’s formula are a good example of this (we only need the cosines).

The first, obvious approach is to to simply evaluate the cosine function using a clever implementation of the Taylor series. For example, we can just call the MPFR cosine function; it is not quite optimal at low precision, but it does implement Brent’s asymptotically fast binary splitting strategy at high precision. For a precision of $b$ bits, the cost is approximately $O(b M(b))$ at low precision and $O(M(b) \log^2 b)$ at high precision. Thus, the complexity is quasi-linear in $b$. Notably, the complexity does not depend on $q$ at all (technically, we do need to add the cost of the multiplication and division when computing $\pi p / q$, but this is not significant). The main drawback of this method is that the $\log^2 b$ factor grows quite large at high precision.

The second approach exploits the fact that a root of unity is an algebraic number and therefore the root of some polynomial with integer coefficients. We can thus refine this root to high precision using Newton’s method, using for instance a low-precision cosine as a starting value. Using a precision that doubles with each iteration up to the final precision, i.e. $\ldots, b / 8, b / 4, b / 2, b$, the total cost is approximately a constant factor times that of evaluating the polynomial (and its derivative) at the final precision $b$. Now many variations are possible, since there are many different polynomials of which $\cos(p\pi/q)$ or $\exp(i p\pi/q)$ is a root.

One variation is to use the natural choice of polynomial $z^q + 1$. The power $z^q$ can be evaluated in $O(\log q)$ steps using binary exponentiation, so the cost is $O(M(b) \log q)$. This is asymptotically superior to evaluating a cosine if $q$ is fixed and $b$ grows. The drawback is that we have to use complex arithmetic. We could also use a cyclotomic polynomial, possibly giving a lower degree, but this does not appear to give any advantage since we lose sparsity.

Another variation is to use the minimal polynomial of $\cos(p\pi/q)$. The advantage is that only real arithmetic has to be used. However, the polynomial in question has degree $O(q)$ and is dense, so if we evaluate it using Horner’s rule, the complexity is $O(M(b) q)$. This is much worse than the complex Newton iteration when $q$ grows. Another disadvantage is that we have to generate the minimal polynomial itself, and it does not have a simple formula, but it turns out that it can be computed quite efficiently using a numerical algorithm: we compute a bound for the coefficients, approximate all the linear factors numerically to sufficient precision, multiply them together using a balanced product tree, and round the resulting floating-point polynomial to an integer polynomial. We could also use a suitably chosen Chebyshev polynomial of which $\cos(p\pi/q)$ is a root, instead of the minimal polynomial. Chebyshev polynomials are much easier to generate than the minimal polynomials, but they will generally be larger, so we lose efficiency at high precision.

In my FLINT implementation of the partition function, I ended up implementing a hybrid algorithm using the trigonometric function at low precision or large $q$, and the real minimal polynomial Newton iteration at high precision and small $q$. I briefly experimented with the complex Newton iteration, but found that it did not help for the distribution of precisions and denominators encountered in Rademacher formula.

In Arb, I have recently implemented the complex Newton iteration along with an improved version of the real minimal polynomial Newton iteration. The two improvements are the following:

Worth noting is that the Newton code in Arb computes rigorous error bounds. I will not go into details too much, but essentially, given a bound for the real Newton iterate $x_n$, one can bound the error of $x_{n+1}$ if the first and second derivative of the polynomial are known on an interval containing $x_n, x_{n+1}$ and the root (an analogous statement holds for complex Newton iteration). The real Newton code is reasonably generic: it takes as input the polynomial and an interval isolating the root, and does all error bounding automatically from there, but it does currently require some more information (such an estimate of the number of guard bits that should be used to evaluate the polynomial to avoid catastrophic cancellation) in order to achieve full accuracy and not just fail with an error.

Compared to the nonrigorous MPFR-based real Newton code I wrote for the partition function in FLINT, there is unfortunately some more overhead in the Arb code at low precision, caused by the extra error bounding procedures and other factors.

I will now present some timing comparisons of four different algorithms. The first (“cosine”) just uses Arb to evaluate $\cos(p \pi / q)$ (at the core of it calling the MPFR cosine function). The second (“minpoly1+cosine”) is the hybrid algorithm I implemented for the FLINT partition function. The third (“minpoly2″) is the improved real minimal polynomial Newton iteration in Arb. The fourth (“complex”) is the complex Newton iteration in Arb.

First out is a comparison done at a fixed precision of 1000 decimal digits. The x axis is the denominator $q$ and the y axis is the time in milliseconds:

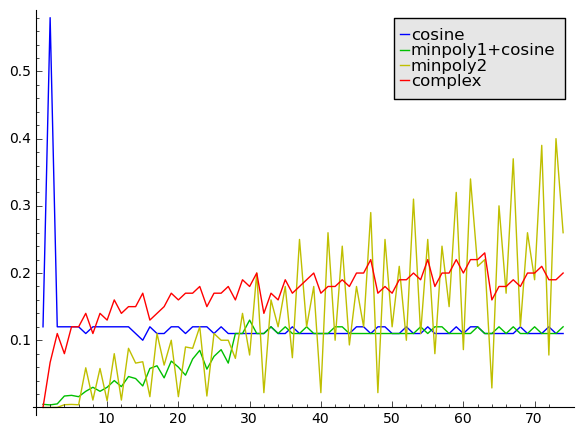
1000 digits

At this precision, the complex Newton iteration never wins. On average, real Newton iteration is faster than the MPFR cosine for denominators up to about 30. The cutoff in FLINT seems quite accurate, as from there on the green graph aligns with the blue one. As expected, the yellow graph visibly dips down when $q$ is divisible by a large power of two, such as $q = 24, 32, 36, 40, 48, 56, 60, 64, 72$, thanks to the half-angle reduction trick.

Next, 10000 digits (again the x axis is the denominator $q$ and the y axis is the time in milliseconds):

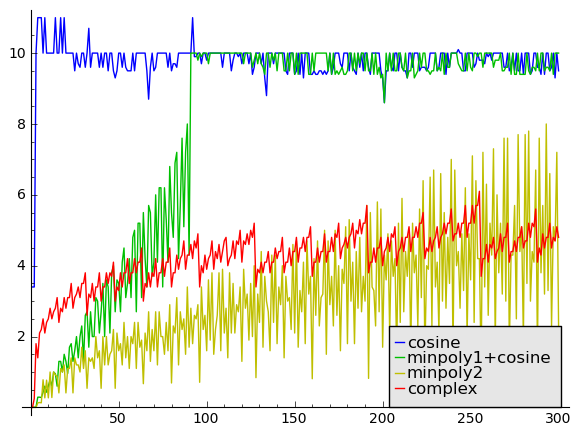
10000 digits

Here we see that the algorithm selection cutoff in FLINT could have been slightly higher at this precision (around 150 instead of 100), but it is not a big deal. What is interesting that the asymptotics are starting to become very clear. The cosine evaluation of course costs the same regardless of $q$. The complexity of the FLINT Newton code can clearly be seen to grow roughly linearly with $q$ (due to Horner polynomial evaluation). The improved Newton code in Arb does seem to grow roughly like $\sqrt q$ (due to the rectangular splitting polynomial evaluation), and the complex Newton code does seem to grow roughly like $\log q$ (due to the binary exponentiation), all agreeing perfectly with theory. If we extended the graph to the right, we would find “minpoly2″ becoming slower than “cosine” at $q = 600$ or so, and “complex” becoming slower than “cosine” at $q = 2000$ or so.

We can even explain the oscillations in the graph: the complex binary exponentiation requires slightly different numbers of multiplications and squarings depending on the bit pattern of $q$ (note for example that the time drops significantly at $q = 96, 128, 160, 256$, where we mostly have to perform squarings), and the more rapid variation of the minpoly algorithm is explained by the variable divisibility of $q$ by powers of two, combined with the fact that the minimal polynomials have variable degree (to be perfectly precise, the degree of the minimal polynomial of $\cos(2\pi/n)$ for $n \ge 3$ is $\phi(n) / 2$ where $\phi(n)$ is the Euler totient function).

We also see that Newton iteration (in any form) really is starting to pay off: for smallish $q$, it is an order of magnitude faster than just evaluating the cosine.

Finally, a comparison at 100000 digits, also looking at slightly larger $q$:

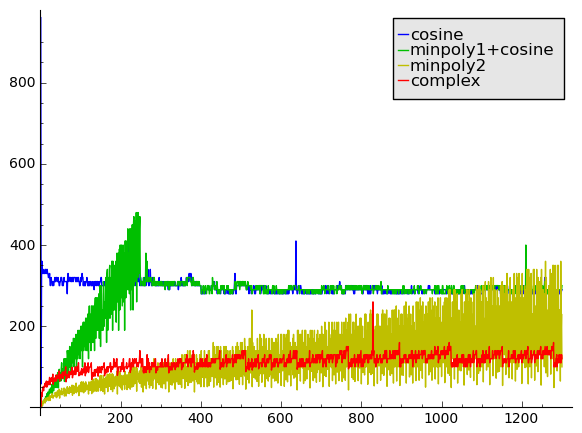
100000 digits

We see the same trends as before (the spikes are probably just noise).

To summarize, as $q$ grows, the minimial polynomial Newton iteration is asymptotically slower than the complex Newton iteration, but it has less overhead over a rather substantial range. It is vital to use rectangular splitting instead of Horner’s rule.

The next version of Arb will contain code for evaluating $\exp(i \pi x)$, $\sin(\pi x)$ or $\cos(\pi x)$ for rational $x$ which automatically selects nearly optimally between the cosine, real and complex Newton algorithms for all precisions and denominators. Longer term, if I find the time, I will also implement faster low-precision sine/cosine functions for general real arguments.



fredrikj.net  |  Blog index  |  RSS feed  |  Follow me on Mastodon  |  Become a sponsor