More digits of zetazero(1)

August 4, 2013

As mentioned in the earlier post about computing 100,000 digits of $\rho_1$, the first nontrivial zero of the Riemann zeta function, the code wasn’t quite optimal.

The expensive part of computing $\zeta(s)$ is evaluating $\sum_{k=1}^N k^{-s}$ for some large integer $N$. When not computing any derivatives, I already exploited the fact that the power $k^{-s}$ only needs to be computed from scratch when $k$ is prime, since we can use $(i j)^{-s} = i^{-s} j^{-s}$ when $k = ij$. So by storing powers in a table, we can greatly improve speed at the cost of memory efficiency (the space complexity becomes quadratic in the precision).

I have now implemented this trick for (short) power series as well, along with some small enhancements to the code. Another small speedup comes from computing logarithms of nearby primes using binary splitting. Finally, I improved the computation of the Riemann-Siegel theta function a bit by using the log gamma and digamma functions directly instead of using the less-optimized log gamma power series code (this change has not yet been committed).

Here are the old and new timings (in seconds) for $\rho_1$ and $\zeta(\rho_1)$:

Digits	Old code		New code
	$\rho_1$	$\zeta(\rho_1)$	$\rho_1$	$\zeta(\rho_1)$
10,000	159	20	24	12
100,000	55,507	5182	5515	2749

Computing $\rho_1$ to 100,000 digits got 10x faster, and the following single evaluation of $\zeta(\rho_1)$ for verification got 1.9x faster. Not bad! At 10,000 digits, Arb is now 141x / 51x faster than Mathematica and 274x / 18x faster than mpmath.

To push the limits a bit further, I’ve now computed $\rho_1$ to 303,000 digits, or just over 1 million bits. This took 73,225 seconds (20 hours) on a CPU about 20% slower (2.00 GHz Xeon E5-2650) than the one used for the benchmarks above. The computation used up to 62 GiB of memory, and involved generating all the Bernoulli numbers up to $B_{325,328}$ as exact fractions! Evaluating $\zeta(\rho_1)$ to the same precision afterwards for verification took 31,772 seconds (9 hours).

The number is available for download:

The imaginary part of $\rho_1$ printed in decimal (all 303,007 included digits are correct)
The computed ball (midpoint mantissa, midpoint exponent, radius mantissa, radius exponent)

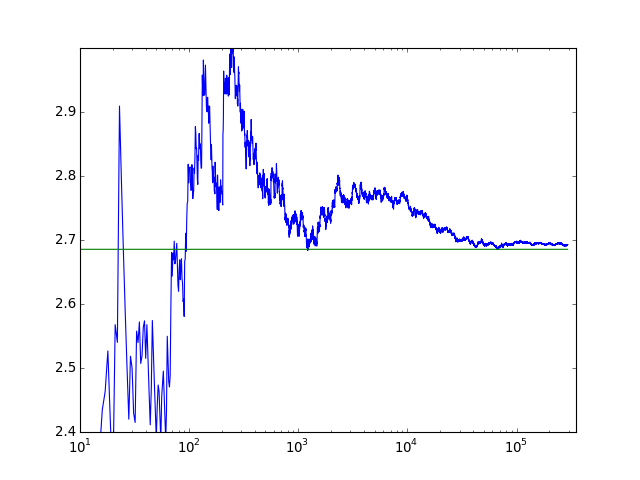
Update: here also is a plot of the geometric means of the continued fraction, suggesting convergence to Khinchin’s constant:

It should be possible to calculate 1 million digits, assuming that one has 600 GiB of RAM and 1-2 weeks of patience. A better way to do that would be to write a parallel and more memory-efficient version, though. The power sum could obviously be done in parallel (perhaps without any sieving to avoid the quadratic memory consumption, or with partial sieving to get a better speed/memory tradeoff). The tail in the Euler-Maclaurin summation formula should be possible to parallelize as well, though that’s slightly more involved (Arb already provides the necessary tools to distribute the computation of Bernoulli numbers).

Remaining potential improvements that come to mind are:

Using Gauss/Karatsuba multiplication to speed up the complex number/power series arithmetic
Using a more complicated sieving strategy to collect small factors (e.g. 3 and 5) in the power sum
Using complex Newton iteration for $\rho_1$ to avoid evaluating the log gamma function altogether
Using approximations instead of exact values for the high-index Bernoulli numbers

More interesting (and useful) would be to thoroughly optimize for low precision (up to a couple hundred digits) and for large imaginary parts (by implementing the Riemann-Siegel expansion). This is a big project, and I doubt I will have time to work on it any time soon!

In related news, I have also added a function that calculates Glaisher’s constant $A = \exp(1/12 – \zeta’(-1))$. Thus another table of timings (in seconds) must be shown:

Digits	Mathematica	mpmath	Arb
1000	0.59	0.40	0.080
10,000	181	98	5.6
100,000	?	?	1182

Wee see that evaluating $\zeta’(s)$ at an integer is slightly faster than at a generic complex number.

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor