fredrikj.net / blog /

Arb 2.0 preview: intervals at the speed of points

May 11, 2014

The forthcoming Arb 2.0 will feature a new floating-point type arf_t and a new ball interval type arb_t with better performance than the present fmpr_t and fmprb_t types.

Arb 1.0 did achieve the goal of providing interval arithmetic with negligible overhead compared to floating-point arithmetic... at precisions in the thousands of digits. Calculations done at more typical precisions of perhaps 10-100 digits could be a factor 2-4 slower in the worst case . Arb 2.0 is intended to bring this down to a factor 1.0-1.2.

I'm pleased to report that work on the new types is going very well. The new arb_t ball type is already complete except for transcendental functions. I will probably implement transcendental functions initially by wrapping the fmprb_t versions, and only speeding them up later. Complex numbers, polynomials and matrices should be fairly easy to port to the new types at this point.

Below, I've benchmarked various arithmetic operations with the old and new types. The plots show time normalized against MPFR (lower is better). Red is old types, blue is new. The thick solid lines show the cost of ball arithmetic (fmprb_t, arb_t), and the thin dashed lines show the cost of floating-point arithmetic (fmpr_t, arf_t) to give an idea of how much time is wasted on propagating error bounds.

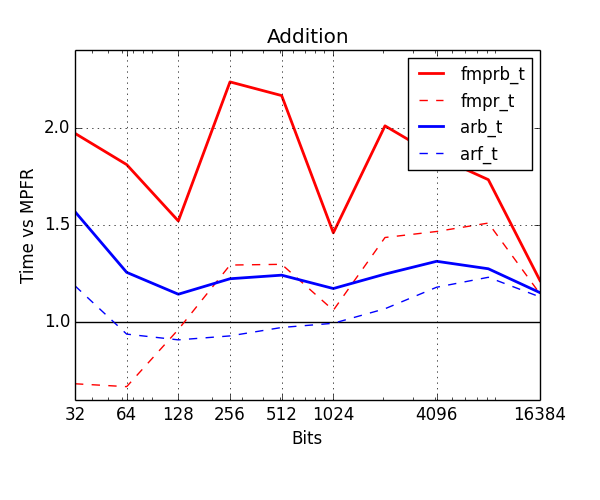
Addition is now typically no more than 20% slower than MPFR. Note that fmpr_t special-cases addition up to 64 bits, which is why it is significantly faster than all other types in this range. I will also implement this optimization for the arf_t type in the future.

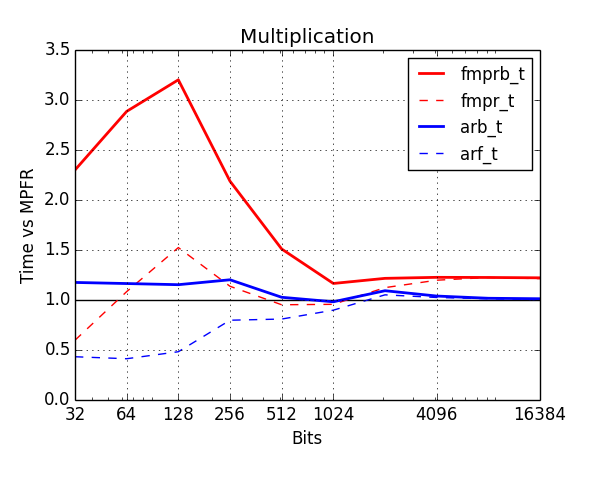
The improvement for multiplication is huge. This could be as much as three times slower than MPFR with the fmprb_t type, but like addition, it is now within 20% even at low precision, where propagating error bounds is a lot of extra work (if the input balls are $[x \pm r_x], [y \pm r_y]$, one has to compute $[xy \pm (|x|r_y + |y|r_x + r_x r_y+\varepsilon_{\text{rounding}})]$ rather than just $xy$). Note also that from about 2048 bits and above, arf_mul now also piggybacks on MPFR's mulhigh code, giving a 20% improvement at precisions in the thousands of digits.

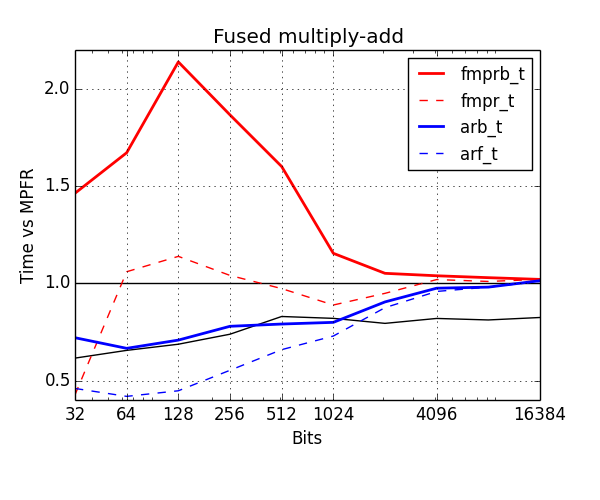
The most important operation is fused multiply-add or addmul, i.e. computing $z \gets z + xy$. This is the building block of matrix multiplication, classical polynomial multiplication, and many other things. In this plot, I have used the cost of mpfr_fma as the baseline, but this function is actually much slower than doing an inexact mpfr_mul followed by an mpfr_add (assuming that you already have a temporary variable allocated), illustrated by the lower black curve. This problem was discussed at the MPFR-MPC developers meeting back in January, and should hopefully be fixed in a future version of MPFR. Anyway, the new arb_addmul is much faster than fmprb_addmul. Unlike arf_mul/arb_mul, it does not implement the mulhigh trick yet (to be added in the future).

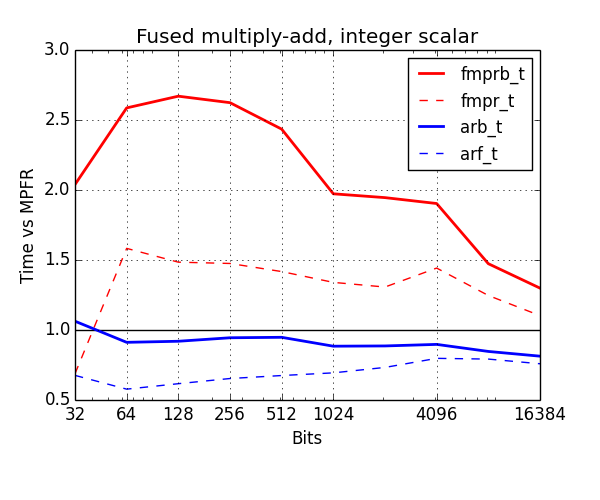
An important variation is to compute $z \gets z + nx$ where $n$ is a fixed word-size integer. Here I used mpfr_mul_ui+mpfr_add with a preallocated temporary as the baseline. Once again, there's a significant improvement for the arb_t type.

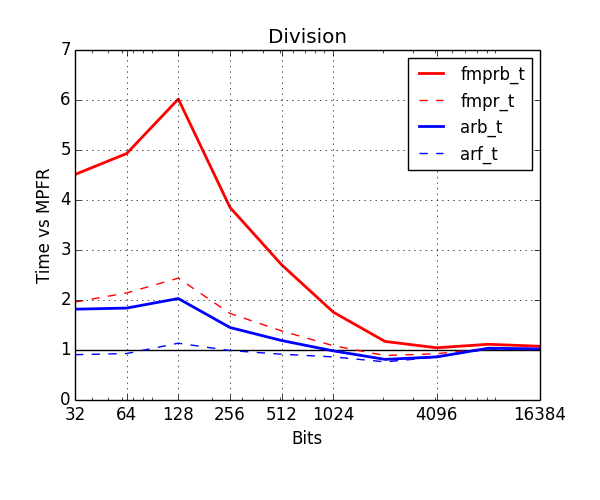
Division has been improved a lot as well. The new arb_div is at most two times slower than the raw floating-point division and comes close around 100 digits of precision (compared to "six times slower" and "1000 digits" for fmprb_div). Most of the speedup comes from computing error bounds faster, and removing general overhead. I don't see an easy way to get rid of the remaining overhead, but it might be possible.

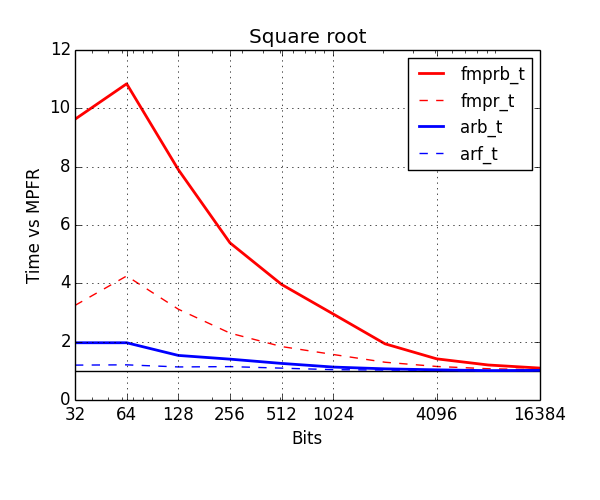
Finally, the improvement for square roots is similar to that for division.

fredrikj.net  |  Blog index  |  RSS feed  |  Follow me on Mastodon  |  Become a sponsor