Faster exp, sin and cos at high precision

September 6, 2017

The elementary functions in Arb are basically implemented using two different algorithms: a basecase algorithm for low to moderate precision, and an asymptotically fast algorithm for arbitrary precision. This applies to the four core elementary functions exp(), sin_cos(), log(), and atan(); other elementary functions are implemented by rewriting them in terms of the core four.

The basecase algorithm was described in my ARITH 2015 paper Efficient implementation of elementary functions in the medium-precision range. Argument reduction is first done using precomputed lookup tables, and the Taylor series is then evaluated using rectangular splitting. The entire computation is done using the mpn layer of GMP to minimize overhead. The basecase algorithm is used up to 4608 bits of internal precision.

(Footnote: the 4608-bit limit is due to the lookup tables being hardcoded, with a total footprint of 240 KB for all functions. In principle, the tables could be generated dynamically, allowing different tradeoffs between speed and memory usage. However, there is not that much to gain by using tables at higher precision, and I'm not keen to add more tuning knobs instead of having a good default that just works. The current table configuration was very carefully considered. Of course, this design could still be revisited in the future.)

The asymptotically fast algorithm for for exp() and atan() consists of what is known as the bit-burst strategy. The idea is to extract 1, 2, 4, 8, 16, ... bits from the binary expansion of the argument and compute the function of each reduced argument using binary splitting. This yields an algorithm with (quasi-)optimal asymptotic complexity. For both sin_cos() and log(), Arb would simply call MPFR. MPFR uses the bit burst strategy for sin_cos(), and the arithmetic-geometric mean iteration for log().

In the past few days, I have made some improvements:

For exp(), a new implementation of rectangular splitting is used in an intermediate range from 4609 bits to 19000 bits. This smooths out the transition from the basecase algorithm to the asymptotically fast bit-burst algorithm. This algorithm is implemented generically using arb_t arithmetic since overhead is not a concern at such high precision; in fact this approach should be slightly faster than mpn code in this range since arb_t multiplications at high precision use the mulhigh algorithm (thanks to wrapping MPFR's mpfr_mul). Argument reduction is done on the fly without requiring lookup tables.
For sin_cos(), the bit-burst algorithm has now been implemented natively in Arb instead of calling MPFR. As for exp(), a generic version of the rectangular splitting strategy has also been implemented in the transition region, which is slightly larger for sin_cos() extending from 4609 bits and all the way up to 90000 bits.

The following plot shows the time to compute exp() at precisions between 10 and 1000000 bits. All times has been normalized by the time for a single call to GMP's mpn_mul_n with numbers of the same bit size; i.e. a time of 50 indicates that computing exp() costs as much as doing 50 GMP multiplications.

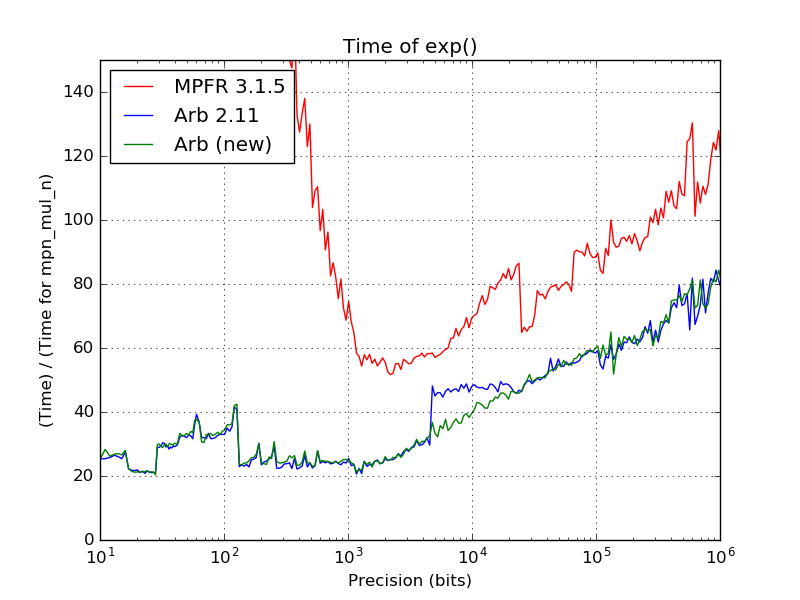
The improvement from the last Arb version (2.11) to the current git code is clearly visible: the jump when switching algorithms at 4609 bits has disappeared completely. The speedup over the old code is about 30% right at the transition point. Although the affected precision range is relatively narrow, this improvement is still quite nice when you happen to be working in that particular range.

MPFR 3.1.5 is included in the plot for scale; MPFR is about 30-40% slower asymptotically (mainly due to some inefficiencies in its binary splitting code) and has far higher overhead at low precision (since it does not have a similarly optimized basecase algorithm).

The following plot shows the time to compute sin_cos(), measured the same way:

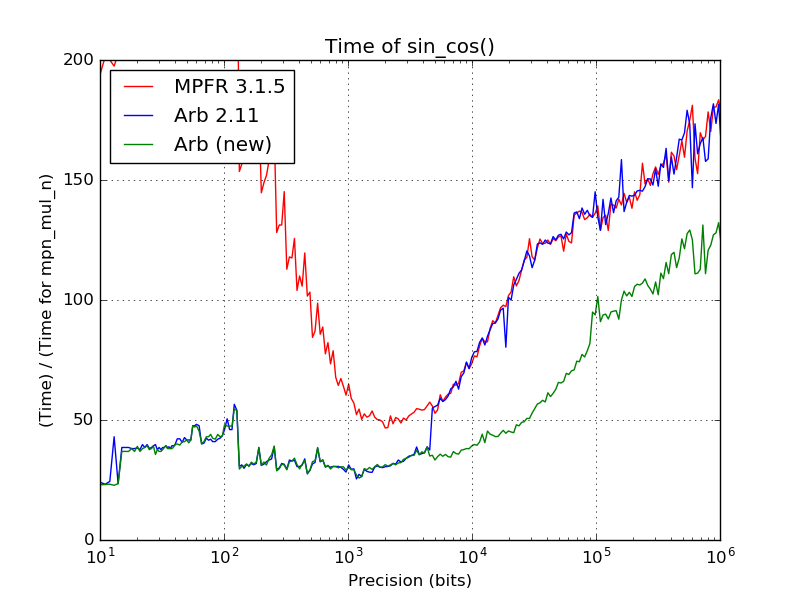
The new asymptotically fast code is about 30-40% faster than MPFR (as well as the old code in Arb which just called MPFR). The jump at 4609 is again eliminated, and there is a particularly nice improvement in the range where the new rectangular splitting code is used; around 30000 bits (10000 decimal digits) it is twice as fast.

These speedups immediately transfer to other functions that depend on computing exponentials or trigonometric functions (the speedup of course depends on the fraction of work spent in those functions). For example consider computing the first zero of the Riemann zeta function to 10000 digits. With Arb 2.11:

> build/examples/real_roots 0 14 15 -refine 10000
...
Function evaluations: 188
cpu/wall(s): 15.878 16.038
virt/peak/res/peak(MB): 57.93 57.93 34.91 34.91

With the new code:

> build/examples/real_roots 0 14 15 -refine 10000
...
Function evaluations: 188
cpu/wall(s): 11.634 11.626
virt/peak/res/peak(MB): 57.93 57.93 34.84 34.84

That is a 35% improvement for a function that does much more than just computing sines and cosines internally.

As two more data points involving more complex tasks, the time to compute the number of partitions of 10¹⁵ dropped from 565 seconds to 535 seconds (a 5% improvement), and the time to compute the Hilbert class polynomial of discriminant −10⁷ − 3 dropped from 20 seconds to 17 seconds (a 15% improvement).

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor