fredrikj.net / blog /

mpmath 1.0, and a ten-year retrospective

October 2, 2017

Version 0.1 of mpmath was released on September 27, 2007. To celebrate the ten year anniversary, I went ahead and released mpmath 1.0 this September 27 instead of issuing the overdue 0.20 (version 0.19 came out three years ago).

As usual, the updates are listed in CHANGES. There are the standard bugfixes and small improvements, thanks to several contributors. The major new functionality in this version is code for computing inverse Laplace transforms, contributed by Kris Kuhlman. Here is an example:

>>> from mpmath import *
>>> mp.dps = 50; mp.pretty = True
>>> invertlaplace(lambda z: 1/sqrt(z**2+1), pi)
-0.30424217764409386420203491281770492396965053478389
>>> besselj(0, pi)
-0.30424217764409386420203491281770492396965053478389
>>> quad(lambda t: besselj(0,t) * exp(-pi*t), [0,inf])  # forward Laplace transform
0.30331447105335286401972407605506801782652930097141
>>> 1/sqrt(pi**2+1)
0.30331447105335286401972407605506801782652930097141

There's not really anything radically new in mpmath 1.0 to prompt a major version number (although the inverse Laplace transform code happens to be a very nice addition). There are also some warts left in mpmath that I would rather have seen fixed. The 1.0 version number just reflects the fact that mpmath is widely used and has been stable for the better part of a decade. I'm one of mpmath's biggest users myself, and the warts are at least minor enough that they don't bother me much in practice, or at least I've just learned to work around the problems and I'm now too lazy to fix them properly!

This year marks not only the tenth anniversary of mpmath, but also my tenth year working on open source mathematical software. Precisely at the halfway point, in September 2012, I released the first version of Arb. (Curiously, 2007 seems like an eternity ago but 2012 is virtually yesterday.) In this extended blog post, I will provide a personal retrospective of the last ten years and attempt to answer the following questions:

This will be a gratuitously detailed personal account, not just technical content, but hey -- that's what a blog is for (you have been warned).

A long history of mpmath

First, why Python? I started learning programming in C when I was around 14. At some point, I asked an internet acquaintance and esoteric programming language enthusiast (user "Lament" from the Doomworld Forums) over IRC what he thought was the best programming language. He replied "dunno, python maybe" and I gave it a shot. Python was a big step up in productivity compared to C due to features like dict, having no malloc/free, no deciphering pointers to arrays of pointers, being able to put any objects inside containers, being able to print anything, not having to bother with compilers and linkers, and not having to type semicolons and braces everywhere... I picked up Python, and abandoned my attempts to become proficient in C. Like many aspiring coders at that age, I was mostly interested in game programming: my first serious projects were a 2D platform game engine (never released) written using Pygame, and Omgifol, a Python library for editing Doom WAD files which is still being used (maintained by others).

In 2004–2006, during my first years in university, I tried to write a computer algebra system in Python as a hobby. It was really just a loose collection of naive algorithms for things like primality testing, computing pi, and basic manipulation of symbolic expressions. My goal was to make something more integrated and useful for general symbolic computation, but I had no idea what I was doing and naturally didn't succeed. Then in early 2007 I found out about a new project called SymPy, headed by Ondrej Certik, which seemed to be exactly what I was looking for. I joined the SymPy team and contributed a bunch of code, most importantly the sympy.numerics module which featured arbitrary-precision floating-point numbers, evaluation of some special functions, root-finding, and numerical integration. It soon made sense to spin off sympy.numerics to a separate project, so I created the Google Code SVN repository for mpmath, and on September 27, 2007, version 0.1 was released. Some of the code had been written before I got involved with SymPy, but it was much thanks to the practical experience with SymPy (including proper use of of version control and unit tests) that I could make a working library out of it.

When I started sympy.numerics, Python already had the arbitrary-precision Decimal type in the standard library, but I found that it was a lot more efficient to emulate binary floating-point arithmetic using Python's arbitrary-precision long integers. It was especially fast to do fixed-point arithmetic this way: an addition is just an addition, and a multiplication (a * b) >> shift requires just one extra operation, whereas a floating-point operation with rounding requires something like 50 Python bytecode instructions. Implementing core operations (like elementary functions) mostly using fixed-point arithmetic internally made it possible to achieve reasonable performance. Once I had implemented basic floating-point operations and elementary transcendental functions, it was easy to add higher features: more transcendental functions, calculus operations, plotting, etc. The interface was loosely inspired by Matlab, designed to support easy use as an interactive calculator via the Python REPL.

How did I end up in that particular niche?

I've been asked a few times how I got into computer algebra, arbitrary-precision arithmetic and special functions, since these are not really topics that you would encounter (more than superficially) as a student. I'm not exactly sure how I became interested in computer algebra to begin with, but reading Structure and Interpretation of Computer Programs and browsing Volume 2 of The Art of Computer Programming as an impressionable 19 year old might have had something to do with it. Part of the appeal was the challenge of working on a really complex system, combining programming with mathematics.

Another concrete factor was using Mathematica and Maple at university. I was intrigued by being able to input some hopeless integral or infinite series, getting a closed-form hypergeometric function or polylogarithm monstrosity back, and then being able to check that both expressions agreed by evaluating them numerically to a thousand digits! I wanted to understand how that worked, and I wanted to be able to write my own code that did the same thing. There is also the practical matter that I'm terrible at calculating by hand, so I'm more than happy to program a computer to do it for me.

For the record, I studied Software Engineering in my first year of university (2004--2005), but switched to Engineering Physics in my second year since I wanted to do more math (not to mention the obvious appeal of black holes and lasers). I should really have gone with physics from the start, but I was too much into programming coming out of high school, and I thought physics would be too difficult for me anyway. It was only after getting through the first year of Software Engineering without any real difficulties that I gained the confidence to switch.

Obviously getting a solid grounding in topics like complex analysis and numerical analysis from undergraduate classes turned out to be very useful, but I was largely self-motivated (and self-taught) when it came to developing mathematical software. It was fun to test the occasional computational example from PDEs, Fourier analysis, functional analysis, quantum mechanics, etc. with mpmath/SymPy, but that was really icing on the cake; I was mainly interested in coding for its own sake rather than in any particular scientific or engineering application.

I need to mention four particularly enlightening books which I bought in 2006: Experimentation in Mathematics and Mathematics by Experiment by David Bailey and the late Jonathan Borwein, Pi and the AGM by Jonathan and Peter Borwein, and Prime Numbers: A Computational Perspective by Richard Crandall and Carl Pomerance. A lot of the ideas and algorithms behind mpmath came from the sections on high-precision arithmetic and special functions in these books. Just to give one example, I learned about the tanh-sinh (double exponential) method for numerical integration from David Bailey's writings. As the default algorithm for mpmath.quad(), it is one of the absolute cornerstones in mpmath.

Other helpful resources included the Numbers, constants and computation website by Xavier Gourdon and Pascal Sebah, Eric Weisstein's MathWorld, and of course Wikipedia (which I was editing very actively until 2005).

Continued development of SymPy and mpmath

Through 2007 and 2008, I continued working actively on both SymPy and mpmath. In 2008, I took part in Google Summer of Code, where my project was to implement numerical evaluation of symbolic expressions. I tried to provide automatic protection against loss of accuracy using something resembling Mathematica's significance arithmetic. Looking back, I'm not really happy with this code. I think Mathematica's significance arithmetic is fundamentally unsound and the wrong approach to doing real number arithmetic, and the way I implemented it was far from elegant (or even fully correct). However, it worked decently well for SymPy's purposes.

Around 2008, several other persons also helped improve mpmath in crucial ways. For example, Mario Pernici made a lot of enhancements to basic arithmetic, implemented asymptotically faster algorithms for elementary functions, and added other new features too. Mike Taschuk wrote the initial code for elliptic functions and Jacobi theta functions (which Mario Pernici then substantially improved). Vinzent Steinberg implemented matrices, basic linear algebra, and a suite of root-finding algorithms.

Case Van Horsen added support for using GMPY as a backend. As mentioned earlier, mpmath fundamentally builds its arithmetic on Python's long type, which allows it to work as a pure Python library without depending on any C extension modules. Thanks to Python's dynamic nature, it turned out that gmpy.mpz (which is much faster than Python's long for very large integers) could be used as a drop-in replacement, with barely any changes to the code. If GMPY is installed, mpmath detects it automatically and switches to gmpy.mpz behind the scenes, completely transparently to the user. Case Van Horsen helped further by adding some utility functions to GMPY related to floating-point rounding and normalization, specifically to speed up mpmath (eliminating some of those 50 bytecode instructions mentioned earlier).

I stopped being actively involved in SymPy development in 2009, though I did add some paragraphs (mostly about mpmath) to the recently published SymPy paper. Just as an aside, it's interesting how SymPy has thrived as an open source project for more than a decade, with many contributors, successful GSoC projects, etc. I think there are two main reasons for this. First, as a computer algebra system written in pure Python, SymPy hits a sweet spot in terms of ease of development and practical utility for many people, despite the existence of software that does some of the same things better on a purely technical level ("worse is better"). Second, SymPy has had a friendly developer community and good leadership: open, pragmatic, and supportive for newcomers. The mpmath library is somewhat too small to attract a persistent developer community of its own (or perhaps I just haven't put in the work to maintain such a community), but it has remained a satellite project of SymPy in some sense, and that has certainly been beneficial.

Enter Sage

In 2008, Sage already had a lot of momentum behind it. Sage was a much bigger and more ambitious project than SymPy, with somewhat different goals. For one thing, SymPy was intended as a simple pure Python library without external dependencies, while Sage wrapped other mathematical software and the kitchen sink (SymPy included) in order to compete head on with the closed source Ma's (Magma, Mathematica, Maple, Matlab). Sage was also mainly being developed by mathematicians, while SymPy was being developed by physicists, which meant that Sage had much more sophisticated tools for group theory, number theory, and so on (on the other hand, Sage had relatively poor support for symbolic calculus, which physicists care about much more than mathematicians). Another nice aspect of Sage was the use of Cython, which allowed writing high performance code without many of the hassles of working with C directly.

February 2009, I got this email from Sage's creator William Stein (this was in response to a CC'ed email from Michael Abshoff after I had asked for Sage Trac access to work on some issue):

Hi, Fredrik, are you the mpmath guy?  Mike Hansen and I were looking
at mpmath -- which is in Sage via sympy -- for a while at Sage Days
12, and we both thought it would be *very* good if it got used more in
Sage.  I'm very glad you're interested in getting this going.   Mike
and I thought a little about how to hack mpmath to speed it up so that
it would work with Sage integers (since we don't ship gmpy).

Here is a typical example of the sort of bug that could be nicely
fixed using mpmath:

http://trac.sagemath.org/sage_trac/ticket/4807

There are problems with Sage's Ei function, where mpmath is way
better, since Sage's Ei function just wraps scipy's and scipy's has
some problems:
   (1) it is buggy, as illustrated by #4807
   (2) it is only double precision, whereas mpmath's Ei is arbitrary precision

Anyway, there are many similar situations in Sage, I think, where --
as Michael says -- Sage's use of scipy/pari/maxima for evaluating
special functions leaves something to be desired.

Shortly after this, mpmath became a standard Sage package, and two other important things also happened:

First, William Stein ended up spending some of his NSF grant money to pay me to work on mpmath and Sage during the summer of 2009. This was essentially just like doing a GSoC project (with the same pay), but without having to go through the GSoC application process. I got to do such a project again in summer 2010. These summers allowed me to work on some features that vastly improved mpmath's usefulness for serious mathematical computations, most notably the full implementation of generalized hypergeometric functions and the Meijer G-function. I also wrote a new GMP backend in Cython for mpmath in Sage, similar to the GMPY backend but even more efficient. As part of this project, I made a major and painful rewrite of the mpmath internals to simplify the handling of different backends. Around this time, Juan Arias de Reyna notably also contributed his implementation of the Riemann-Siegel formula and Turing's method for locating zeros of the Riemann zeta function, and I helped a bit with that project.

Second, William invited me to Sage Days 15 which took place at the University of Washington in Seattle in May 2009. This was my first conference and the first time I traveled abroad on my own. I would also be invited to two more Sage Days the next year: SD23 at the Lorentz Center in Leiden, and SD24 at RISC in Linz, Austria. It was very nice to meet other developers, including future colleagues, and the Sage Days overall made a good impression.

On to FLINT

At SD15 in Seattle, I met Bill Hart, the lead developer of FLINT, for the first time. Bill Hart gave a talk where he showed off the $\mathbb{Z}[x]$ multiplication code in FLINT that he had developed together with David Harvey, by some margin the fastest code in the world for this purpose at the time. This blew me away. I already knew about asymptotically fast algorithms, of course, but that was all very abstract; here it turned out that you could literally multiply two polynomials with a million bits of data faster than you could even boot up a Python interpreter. Heck, multiplying polynomials several gigabytes large was no problem whatsoever!

FLINT interested me for two particular reasons related to mpmath. First of all, fast polynomial multiplication can be used for power series manipulation, which is very handy for arbitrary-precision numerical computing. Fast power series techniques would allow solving certain bottlenecks that appeared in mpmath at very high precision (for instance: generating lots of Bernoulli numbers for Euler-Maclaurin summation).

The second reason is a minor technical detail. Bill Hart had implemented a custom multiprecision integer type (fmpz_t) in FLINT that was much faster and more space efficient than the standard GMP mpz_t type for small values. An mpz_t is a two-word data structure that contains a pointer to heap-allocated digit data. For polynomials with small coefficients, FLINT would have taken longer to simply allocate mpz_t's for the result than doing the actual multiplication. To avoid this overhead, FLINT's fmpz_t type stores coefficients up to 62 bits as immediate values in a single word, seamlessly converting to a heap pointer only when needed for larger values. The Cython/GMP backend I was developing for mpmath uses the mpz_t type for all integers that potentially could be bignums, even for the kind of quantities that almost always will be smaller than 64 bits, such as small series coefficients and exponents of floating-point numbers. While the FLINT integer type was designed for polynomial coefficients, I realized that it would speed up mpmath as well.

I never actually ended up using FLINT for the Cython/GMP backend for mpmath in Sage; what happened instead is that I took a break from mpmath and Sage development and began working on FLINT itself in 2010. More precisely, I started helping out with FLINT 2, which was a rewrite of FLINT 1.x from scratch. Bill Hart had first started FLINT 2 as a small private project, but it became much more than that in large part thanks to Sebastian Pancratz (whom I met at SD23 and SD24). Among other things, Sebastian wrote the FLINT 2 fmpq_poly module since he needed a fast $\mathbb{Q}[x]$ implementation for his PhD thesis project, and he also encouraged Bill to make FLINT 2 public.

Facing C

You may recall from the beginning of this story that I started life as a C programmer but gave up on it since I wasn't making much progress and high-level languages like Python looked far more productive. I would frequently find myself reading or modifying C code over the years, of course, and much of the Cython coding which I did for Sage was closer to C than Python, but the thought of doing major feature development in C itself seemed foreign.

FLINT 2 changed all that. FLINT 1.x was a fairly ugly piece of C code, both on a micro and macro level: some aspects of its design had proved to be highly bug-prone, and the organization of the code itself was a bit of a mess. With FLINT 2, Bill Hart tried to make the code as simple and clean as possible as a reaction to the problems with FLINT 1.x (without giving up speed). The FLINT 2 code was beautiful. Neatly structured, obvious, and trivial (even inviting) to extend. On top of that, it had a build system that Just Worked (TM).

As I worked on FLINT 2 during 2010 and 2011, I became proficient with low level programming in C. I also basically learned from the FLINT 2 design how to develop a C codebase that can be scaled indefinitely without succumbing to complexity, using rather simple principles such as the following:

Many of these things sound obvious, but some are actually the polar opposite of what I would be doing in Python at the time. A cynical way to put it is that Python lets you get away with bad design, while C punishes you for it very quickly. (That said, there are also genuine differences in what works best in the respective languages, and for different projects with different goals and constraints.) FLINT 2 is not without its flaws, of course, especially the older parts of it: much of my code from 2010 is certainly subpar by today's standards and I think Bill Hart too has some code from 2009--2010 that he'd rather not be reminded of. Some of the neatness of the early code also vanished as the project grew (and FLINT 2 is fairly large today). But FLINT 2 has held up well overall, and it led to my next major project: Arb.

PhD work and Arb

As I was finishing my master's degree in spring 2010, I started looking around for opportunities to do a PhD, ideally related to computer algebra. I vaguely knew Burcin Erocal, at the time a PhD student at RISC, from the Sage development community. I asked if he was aware of any openings, and he suggested that I write directly to Manuel Kauers, who as it turned out had just been awarded a big grant concerning "Fast Computer Algebra for Special Functions" (the START project). That sounded perfect, and my application was accepted! It was probably in part thanks to having mpmath and Sage development on my CV that I got the chance to do a PhD at RISC: my academic performance to that point was OK but nothing extraordinary and I had very little background in algebra anyway (Engineering Physics is 75% math, but 90% of that is analysis).

In late 2010, when I started as a PhD student, my mpmath-related activity dropped significantly. This happened naturally since I was running into new topics to study, and in any case mpmath worked pretty well as it was. I was also increasingly coming to the realization that many deficiencies in mpmath could not be solved incrementally but required a fundamentally new approach (more about this in a moment). Anyway, during my first year or so as a PhD student, I spent a lot of time studying core algorithms for computer algebra and writing implementations for FLINT. I was no longer doing anything numerical: everything involved the exact ground domains ($\mathbb{Z}, \mathbb{Q}, \mathbb{Z}/n\mathbb{Z}, \ldots$) available in FLINT.

There is a traditional divide in computational mathematics between symbolic computation with exact numbers (e.g. rationals) and numerical computing with real and complex numbers. With exact domains, your answer is either correct or dead wrong. In numerical computing, your answer might be slightly wrong... and then you fudge your way around it with some heuristic solution. This heuristic approach gives you a lot of leeway, but it has a big drawback: for every bug you "fix", there is probably still going to be another one, just more obscure. This had always been a problem when developing mpmath.

There is the possibility of doing rigorous error analysis for numerical algorithms, but this doesn't scale. Essentially, the problem is that implied error bounds are not preserved under composition: even if $f(x)$ and $g(x)$ are computed with correct rounding individually, $h(x) = f(x) + g(x)$ is not, and you need to catch all the conditions on $x$ that make $f(x) \approx -g(x)$ to limit the relative error on $h(x)$. The difficulty of developing a correct algorithm based on error analysis can grow quickly when the number of ingredients in the algorithm grows (just like the number of potential bug conditions in a heuristic solution). Error analysis also has the same general problem as code comments. Even if the analysis is correct, nothing guarantees that it matches the actual code, especially over time as code and its dependencies change. When modifying code that depends on existing error analysis, the analysis has to be updated or at least reviewed to make sure that all conditions assumed in the analysis are satisfied.

A year or so into my PhD, I had a number of problems I wanted to solve with FLINT that would require numerical computations. I was getting tired of fudging (which certainly had proved to result in bugs in the past), and error analysis was not going to scale. A concrete example was computing the partition function: I wrote a fast implementation for FLINT using MPFR arithmetic, but it took me a few weeks to do an error analysis (and even then some semi-heuristic estimates were necessary). I also knew some ways to optimize the algorithm further, but they would have required the error analysis to be done anew, which was very annoying.

This is where I realized that I potentially could use ball arithmetic to solve my problems. With ball arithmetic, correct error bounds become an invariant property enforced at the level of datatypes, and this property is preserved automatically under composition. Error analysis might still be needed locally, for example to bound the truncation error in an approximation $$f(x) = \sum_{k=0}^{\infty} T_k(x) \approx \sum_{k=0}^N T_k(x),$$ but the ball arithmetic takes care of propagating error bounds globally, solving the problem of scaling up correctness from small functions to complete programs. This also means that there is a contract which can be tested stringently, much like a falsifiable scientific hypothesis. A unit test can pick a million random inputs, and they can be chosen to be as nasty as possible. If a single computed ball is disjoint from the exact solution, even by a slight bit, then the code is dead wrong. Having such a sharp test is a big advantage when developing complex functionality.

Of course, I did not invent ball arithmetic from scratch. Interval arithmetic was well established, but it is twice as expensive as floating-point arithmetic; with ball arithmetic, it should be possible to get within $1 + \varepsilon$ of arbitrary-precision floating point. I had read some papers by Joris van der Hoeven about ball arithmetic, but it was not an established technique, and I had no idea whether it was going to work in practice. In any case, the available implementations of interval arithmetic (mainly MPFI) and ball arithmetic (mainly Joris van der Hoeven's Mathemagix and the lazy reals library iRRAM, both C++ projects) lacked many of the optimizations and the special functions I wanted in FLINT.

In early 2012, I wrote some experimental ball arithmetic code to try a few test problems like evaluating simple hypergeometric functions and multiplying polynomials. It worked perfectly, so I proceeded to start the Arb library, building on top of FLINT. The arithmetic in Arb was done from scratch using FLINT integer functions instead of using MPFR since this was going to be faster for certain applications (in particular for working with balls actually representing integers). Besides, from my experience developing mpmath, I knew that contrary to MPFR, I did not want the working precision stored in the individual number objects, I did not want signed zero, I did not want global state in the form of exceptions, and I did want built-in arbitrary-precision exponents.

The initial plan was basically to extend FLINT to the ground domains $\mathbb{R}$ and $\mathbb{C}$, providing a complete set of types and methods for numbers, polynomials and matrices including asymptotically fast algorithms for everything just like FLINT did for $\mathbb{Z}$, $\mathbb{Q}$, etc. This was relatvely easy after implementing the basic ball arithmetic. Eventually, with all the fundamentals in place, I was able to re-implement many mpmath transcendental functions in Arb as well, only this time rigorously and much more efficiently. The partition function code and other semi-numerical code I had written for FLINT using MPFR or fixed-point arithmetic also turned out to be very easy to port over to Arb.

Arb 0.1 was released in September 2012. Version 1.0 of Arb was released in late 2013, within 18 months of the initial 0.1 release. Version 2.0, released in mid 2014 (just after I completed my PhD), contained a full core rewrite to improve efficiency. I'm not going to discuss the Arb development history in much further detail here (there is plenty of information in older blog posts), but I do want to point out that the version numbers for Arb were incremented much more rapidly than for mpmath, for a reason: I was much more confident in the design and overall code quality. Even for things that needed a temporary working solution in Arb, I'd have a clear plan for how to fix it later, and I've always been able to go back do exactly that without difficulties. Getting Arb working that smoothly was essentially possible thanks to the combination of several things:

The current state of mpmath

The significant developments for mpmath since about 2011 include:

My own contributions have been marginal apart from merging code and occasionally fixing some bugs. My efforts have largely been focused on FLINT and Arb. Will I ever return to significant feature development in mpmath? I hope so: I do still have a list of things I would like to add or improve in mpmath, particularly things that could not be done in Arb (generally because there is no realistic way to get rigorous error bounds). However, I feel much less motivated to do things in mpmath that I know how to do better in Arb. I feel especially little motivation to do things in mpmath that I've already done better in Arb. Not that those things wouldn't be objectively useful (mpmath has many more users than Arb); the work would just be less intellectually rewarding.

Problems with mpmath

As I've already alluded to, Arb solves two scaling problems inherent in mpmath:

In terms of features, mpmath is missing some essentials such as good support for manipulating polynomials and power series.

Apart from fundamental limitations, there are also some problems with mpmath's internal design that make it harder than necessary to work on. These problems could be addressed with a major code cleanup, but it's uncertain if I will have time to do it. I'm ignoring minor warts (inconsistent naming, abuse of metaprogramming features, lack of internal documentation, etc.) here.

Some of the problems are due to performance hacks. When I created mpmath, I put in a lot of small hacks that individually made a small difference for performance and cumulatively led to perhaps a factor two speed improvement, such as working with raw tuples instead of normal Python objects internally, precomputing the bit lengths of integers, and going through contortions to avoid expensive isinstance calls or attribute lookups. There is even some instance of code generation inside mpmath to avoid the overhead of runtime conditionals and loops. You will note that many of these hacks are just fighting against inefficiencies of the Python interpreter, which is a serious drawback of trying to write performant Python code. Ultimately, the gains are small potatoes compared to simply writing C code which makes things 10 or 100 times faster by default (even if one writes the cleanest possible C code without any performance-enhancing obfuscations).

In retrospect, it might have been better to focus on a cleaner pure Python codebase while giving up some performance, putting more oomph into an optional C extension. That's not to say that optimizing the Python code was the wrong tradeoff at the time. Small savings do matter for numerical applications. Also, back in 2007–2008, I simply didn't have the skills to write such C code myself. Even I had possessed the skills, distributing extension modules was a lot harder than it is today (to make matters worse, I was a Windows user at the time).

Besides certain misguided micro-optimizations, the mpmath codebase also contains a few (overly) clever implementations of what are ultimately not even the best algorithms for the job. It would obviously make sense to just implement better algorithms! However, as I've already mentioned, I have little personal motivation to do this where I've already done (or plan to do) the job properly in Arb.

Things are complicated by the lack of formal guarantees, which can make it hard to discern intended behavior from bugs. For example, someone recently pointed out that a term in the heuristic mpmath uses for error estimation in numerical integration actually is mathematical nonsense since it conflates a $\log_2$ with a $\log_{10}$. However, it turns out that the heuristic somehow works by accident and the obvious "fix" actually breaks or slows down some existing examples. Who knows what external code may be relying on such quirks? The issue of breaking backward compatibility by making subtle changes to numerical algorithms is a delicate one.

Verily, mpmath also has the fundamental problem that it's awkward to start a sentence with. Is it mpmath or Mpmath or even MPmath? I've never thought either looked right. Better awkwardly insert another word before it. Arb works just fine at the start of a sentence. On the other hand, mpmath is more googleable.

The good with mpmath

Despite the problems I've discussed, mpmath works well in its own niche. It's important to step back and remember that while Arb solves some technical problems better, it doesn't encompass mpmath. Ball arithmetic is not a perfect substitute for floating-point arithmetic. It works better for certain types of tasks, but it doesn't work for everything. There are many situations where slightly wrong floating-point approximations are just as useful as provably correct intervals or balls, and where floating-point numbers are easier to use. There are still problems where a heuristic numerical solution can be found easily but where an interval/ball solution would be hard to compute, if an effective interval/ball algorithm is known at all! Of course, I'm hoping to find solutions to such problems as part of my research, but that's a long-term project and it's not going to solve all problems.

Most importantly, mpmath is very easy to install and use. Arb is harder to install (though this is less of a problem nowadays since package managers can do the job) and much harder to write code for. Arb itself has a very low-level interface by design, lacking conveniences like automatic type coercions and operator overloading; it is not designed for interactive use without an intermediate wrapper layer. 100 mpmath one-liners for pi would become 10 Arb 10-liners for pi. Even the function names reflect this difference: names in Arb are highly verbose to make a large codebase easier to understand, while mpmath names are short for easy interactive use (Python namespaces, keyword arguments and dynamic typing also make a big difference, of course). Arb does have high-level interfaces as part of Sage and Nemo, but these interfaces are still a bit less convenient than mpmath for quick calculations.

By any measure, mpmath has been successful. I have no idea just how many users there are, but the number must be in the thousands without even counting indirect use via SymPy and Sage. Scientists and engineers do use mpmath. As I point out on the main page of my website, the diverse applications of mpmath include stellar astrophysics, quantum field theory, antenna design, image processing and computational biology. A search on Google Scholar currently yields 314 mentions of mpmath in the scientific literature, including 84 proper citations of the software itself. I also get the occasional private email where someone tells me that they used mpmath to solve problem XYZ in their research, and that's always nice! (At least two users claim to have solved the Riemann hypothesis.)

Users evidently find that mpmath solves some real problems pretty well. There are Sage users who use mpmath in Sage instead of Sage's builtin RealField, RealIntervalField, etc. simply because they find mpmath easier to work with. Some people use it just for plotting things. Many users will simply never run into any serious bugs, or they will simply find workarounds, just like with any other numerical software. While mpmath is too slow for some research computations, it is certainly good enough for use as an advanced calculator, for prototyping, and for the occasional expensive calculation that just needs to be run once.

Crucially, mpmath fits neatly into the overall scientific Python stack, not just as a dependency of SymPy and Sage but as a standalone Python library that can be used together with NumPy, etc. For example, SciPy uses mpmath for some test code and precomputations (although mpmath is not a dependency of SciPy itself). I've even heard that some people like to put mpmath numbers into NumPy arrays! I could see improved interoperability with NumPy and SciPy as a potential development idea that would benefit a large number of users.

Like most Python libraries, mpmath is very liberally (BSD) licensed, while Arb is licensed LGPL. Some people don't want to touch software if the license has a "G" in it. I would probably prefer to use BSD or MIT for everything, but GMP/MPIR, MPFR and FLINT are all LGPL projects, and that's unlikely to change. GMP/MPIR, MPFR and FLINT are hard dependencies for Arb, so changing the license for Arb itself would make no difference.

I personally use mpmath all the time for prototyping Arb algorithms (among other things). This is part of the reason why C works well as an implementation language for Arb. The difficulty is usually getting the formulas right, identifying the redundant calculations, ironing out the off-by-one errors, etc., which can all be done with rapid prototyping in Python. Ultimately translating the working solution to C tends to be straightforward. Also, if I need to track down a bug in Arb, doing some quick reference computations with mpmath is often a big help.

A future possibility: using Arb to power mpmath?

Some of the work put into Arb could be leveraged for mpmath users by writing an optional Arb based backend for mpmath in Cython. The multiprecision floating-point type arf_t in Arb is feature-equivalent with mpmath.mpf, and all the low-level operations needed by mpmath can be done by Arb, so it should just be a matter of writing very straightforward (but tedious) wrapper code. Wrapping transcendental functions should be relatively easy too. Such a backend could obsolete both the GMPY backend and the current GMP/Cython backend in Sage, as it would be a lot more efficient than either. I don't see myself working on such a backend any time soon since I have many other items in my TODO list, but I would be happy to provide assistance if someone else were to do it.

Another project worth mentioning is python-flint which is a fairly comprehensive Python interface to both FLINT and Arb written in Cython. I use it mainly as a way to test Arb functions interactively (it even supports interaction between mpmath and Arb types). I haven't advertised it much, because the interface is still a bit unpolished, and it's missing test code, documentation and a proper build system. With a bit of work, it could be turned into a user-friendly library. The simplest way to write an Arb backend for mpmath would actually probably be to write some plain Python code around python-flint, though this would be a bit less efficient than separate Cython code designed specifically for an mpmath backend.

Writing code and writing papers

As I mentioned earlier, my mpmath-related activity dropped significantly around the time when I became a PhD student. Since I'm now employed as a researcher, the reality is that, at least to some extent, I need to prioritize work that can lead to new publications over plain software maintenance. An important aspect of Arb is that it has led to a number of publications, including parts of my PhD thesis. It is difficult to publish papers about implementations of mathematical algorithms, especially if the main contribution consists of vague performance claims or merely having an open source alternative to something that can already be solved by closed source systems. It is easier to publish a paper if you can do something asymptotically fast for the first time (even if that does not translate into a practical speedup), and it is much easier to publish a paper if you can do something with mathematical rigor for the first time.

My very first attempt (in 2011) to write a conference paper, describing the implementation of hypergeometric functions in mpmath, was rejected. Two referees gave a positive review, and two gave a negative review, mainly citing lack of novelty. The rejection was fair: it was not a very well written paper, it had some real gaps in the scientific content, and it was probably submitted to the wrong venue anyway. A publishable paper could probably be written on the subject, but that was clearly not the one. Incidentally, hypergeometric functions seem to remain cursed for me: my 2016 paper on hypergeometric functions in Arb was rejected for supposed lack of novelty when I submitted it to a journal last year. An instant rejection by the editor, no less! After having submitted it to a different journal, I'm still waiting for the review one year later, but at least it hasn't been rejected outright. Fortunately, most of my Arb-related papers have been well received by the research community. I did get the "best software presentation" award at ISSAC 2013 (the prize included a nice gömböc courtesy of MapleSoft) and most recently a paper of mine was selected as the best of the issue in the IEEE Transactions of Computers special issue on computer arithmetic (the prize was an invitation to speak at this year's ARITH conference in London).

I have to point to William Stein's excellent account of his troubles funding Sage development. He quotes a great line: "Every great open source math library is built on the ashes of someone's academic career." I think I've been quite lucky since I did my PhD in a place (RISC) where software development was understood to be a useful part of academic research, and I'm now working in a different place (INRIA and the computational number theory group in Bordeaux) where software development is understood to be a useful part of academic research. Unfortunately, such environments still seem to be the exception rather than the rule, and it's hard to predict what my opportunities will look like down the road. An important factor is that I've never had teaching responsibilities. This has given me more time to write code than most academics would be able to afford (I can't imagine writing code, writing papers and teaching, though some people apparently pull off all three). Of course, lacking teaching experience is a major roadblock when applying for most academic positions.

There is also the fact that both mpmath and Arb are small projects that can be run by a single person. It's another problem entirely to take on more difficult projects that would require commitment from a large developer team. The recent grants OpenDreamKit (EU) and OSCAR (Germany) are perhaps a sign of things heading in the right direction, at least in parts of Europe. (For the record, I'm not personally part of either ODK or OSCAR, but I do benefit indirectly from them due to workshop invitations, etc.)

Footnote: commit history

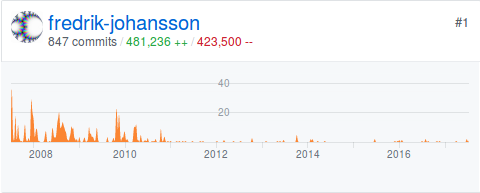
To conclude this ten year retrospective, these GitHub graphs show how my commit activity has changed over time. This is mpmath (most activity 2007-2011):

mpmath commit activity over time

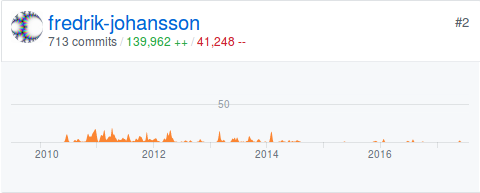
FLINT (most activity 2010-2014):

flint commit activity over time

Finally, Arb (2012-present):

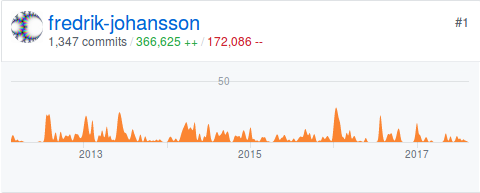
arb commit activity over time

Adding up everything I've worked on in ten years (mpmath, Arb, FLINT, SymPy, Sage, Nemo, python-flint, ore-algebra, and a couple of others), it turns out that I've precisely passed one million "lines added" (by git's way of reckoning), over some 3000 commits. Most of those lines were evidently so bad that they had to go, since I've also racked up 600K "lines removed". Closer inspection shows that about 250K added and removed lines were just for the built HTML docs that were placed in mpmath's then-SVN repository to allow online viewing in the Google Code days. Statistics is the superlative of lies, as they say.



fredrikj.net  |  Blog index  |  RSS feed  |  Follow me on Mastodon  |  Become a sponsor