fredrikj.net / blog /
New rigorous numerical integration in Arb
November 23, 2017
The next version of Arb will introduce the function acb_calc_integrate for computing definite integrals $\int_a^b f(x) dx$ with rigorous error bounds. I already discussed the possibility to use Arb for numerical integration four years ago, but the old toy implementation (which used Taylor series) was both inefficient and hard to use. The new integration code is far more efficient, more general, and easier to use. Combining industrial-grade™ adaptive subdivision with degree-adaptive Gauss-Legendre (GL) quadrature, it achieves near-optimal convergence for holomorphic integrands while being able to cope with a wide range of pathological functions. Minimal extra information is required from the user apart from black-box evaluation of $f$ plus the ability to test for holomorphicity in order to use GL quadrature; in particular, function derivatives and a priori locations of discontinuities are not required. The main limitation is that only proper integrals are supported directly. The integration code supports both absolute and relative accuracy goals and aborts gracefully (and configurably) if convergence is too slow.
In this blog post, I will discuss the algorithm and present several examples of integrals of varying difficulty. The integration code is available in the git master of Arb, with some documentation, and a demo program implementing most of the integrals in this blog post is available as examples/integrals.c.


Principle of operation: (a) old-fashioned heuristic numerical integration, (b) new-fangled rigorous numerical integration.
First of all, why insist on rigorous error bounds? Any integration algorithm that estimates errors heuristically (typically by comparing the result of using two different quadrature rules) can be fooled. The documentation for Mathematica's NIntegrate includes this cautionary example: $$\int_0^1 \operatorname{sech}^2(10(x-0.2)) + \operatorname{sech}^4(100(x-0.4)) + \operatorname{sech}^6(1000(x-0.6)) dx = 0.2108027355\ldots$$
With default settings, Mathematica's NIntegrate outputs the inaccurate value 0.209736, without any warnings (it will compute an accurate result if the user sets a sufficiently high accuracy goal manually). Most numerical software will have similar problems; for example, Sage's numerical_integral and SciPy's scipy.integrate.quad give the same inaccurate result as Mathematica, which is returned along with a bogus error estimate of $10^{-9}$ or $10^{-14}$. Pari/GP's intnum and mpmath's mpmath.quad in turn return different estimates for this integral, each inaccurate beyond the first two or three digits. In fact, Pari/GP still only gets two digits right if the precision is increased to 1000 digits, while mpmath with 1000-digit precision reaches a measly 19 correct digits!
The reason becomes obvious when plotting the integrand:
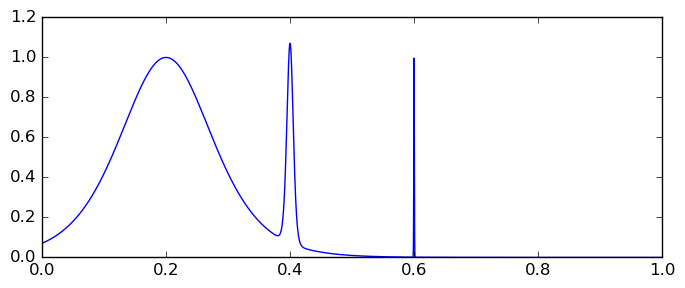
The contributions from the narrow peaks are easily missed when sampling a discrete set of evaluation points. It so happens that the peak at $x = 0.6$ falls right between the cracks of the widely used (7,15)-point Gauss-Kronrod formula, which explains why Mathematica, Sage and SciPy all compute the same wrong answer. The integration algorithm in Arb will not be fooled, however; no such features of the integrand can slip through undetected in interval arithmetic, no matter deviously hidden they are. With 64-bit precision, Arb computes this integral in 0.0051 seconds, giving an accurate enclosure:
[0.21080273550054928 +/- 4.44e-18]
If we just want a few digits, the precision or the accuracy goal can be reduced. Evaluating the integral at 32-bit precision takes 0.0030 seconds, giving:
[0.2108027 +/- 4.21e-8]
Higher precision is no problem. With 333-bit precision, it takes 0.038 seconds, giving:
[0.21080273550054927737564325570572915436090918643678119034785050587872061312814550020505868926155764 +/- 3.72e-99]
With 3333-bit precision, it takes 8.7 seconds, giving:
[0.2108027355005492773756432557057291543609091864367811903478505058787206131281455002050586892615576418256930487967120600184392890901811133114479046741694620315482319853361121180728127354308183506890329305764794971077134710865180873848213386030655588722330743063348785462715319679862273102025621972398282565491985013856696503341146713689475429105189123441532762221073971060163102565201384264539059315164587271771387804560804155713617180157252033458942232730298674239851769812344295889281655702590584995683851507568870377664831323098097088717815845920285011595573800242454588109582117478315402135933455069904617970396287310526667925996015375224731308011614982670381636551677372610623674283628766473235488930347869291768724581256509105460047258808087778746706446723379998322090819265195514605672518269659908006036996478580758785902792878821441064856404559942972745549733148240127257121373225380650636758727660502248127426772955849986119442410239414975142681856841572013309327434544120526904793978249363773 +/- 1.39e-1001]
How it works
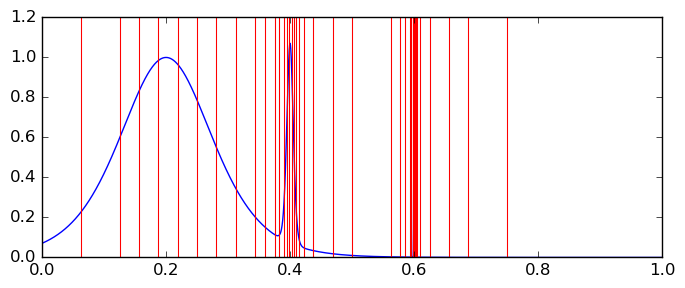
The adaptive integration algorithm in Arb uses repeated bisections to partition the interval $[a,b]$ into smaller subintervals. A subinterval $[a_k,b_k]$ is not split any further when either the direct inclusion $\int_{a_k}^{b_k} f(x) dx \subseteq (b_k - a_k) f([a_k,b_k])$ or a GL quadrature rule of reasonable degree (by default $O(p)$ for $p$-bit precision) meets the error tolerance goal. In the example given above, the splitting terminates on 49 subintervals (down to a width of $2^{-12}$ near $x = 0.6$), and the integrand is evaluated a total of 1299 times for 64-bit precision, 4929 times for 333-bit precision, and 48907 times for 3333-bit precision. This plot shows the domain splitting:
The rigorous implementation of GL quadrature uses complex analysis. If $f$ is holomorphic with $|f| \le M$ on an ellipse $E$ with foci $\pm 1$ whose semiaxes sum to $\rho > 1$, it can be proved that the error of $n$-point GL quadrature on $[-1,1]$ is bounded by $$\left| I - \sum_{k=0}^{n-1} w_k f(x_k) \right| \le \frac{64 M}{15 (\rho-1) \rho^{2n-1}}.$$ For a discussion of such error estimates, see Lloyd N. Trefethen, "Is Gauss Quadrature Better than Clenshaw-Curtis?". Of course, for a general interval or complex line segment $[a_k,b_k]$, one just makes a linear change of variables onto $[-1,1]$ before applying this formula.
Evaluating $f$ on a complex interval containing $E$ gives an upper bound $M$ (the implementation of the integrand must simultaneously test that $f$ really is holomorphic on $E$). A larger $\rho$ improves convergence as $n \to \infty$ but increases $M$, so Arb automatically tests successive larger $\rho$ to attempt to minimize the degree $n$. It can happen that $E$ contains singularities of $f$, which makes $M = \infty$, or that evaluating $f$ on the whole of $E$ in complex interval arithmetic leads to a too pessimistic $M$ even if it is finite. In either case, failing to find $(\rho, n)$ such that the error bound becomes small enough leads the algorithm to proceed by bisecting the interval.
This plot over the complex plane shows the ellipses (blue) which Arb ends up using for the example integral. The poles of the integrand (which lie on three vertical lines) are indicated with red dots.
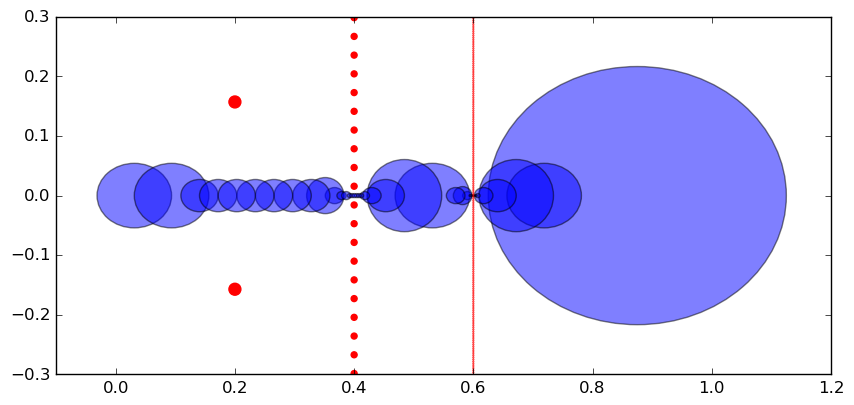
We can see that bad behavior is caused by poles lying close to the integration path, which is a common phenomenon. The poles get caught automatically when evaluating the integrand on complex intervals. An important remark is that the efficiency can be very sensitive to the numerical stability of the algorithm used to evaluate $f$. For example, if $f(x) = 1/g(x)$, the magnitude bound will blow up if the computed complex interval for $1/g(x)$ contains zero, even if $f$ is actually finite on the given complex interval for $x$. In general, one should rewrite integrands so that rapidly growing functions don't appear in denominators: $e^{-x}$ is much better than $1 / e^x$. If we had used acb_cosh followed by acb_div to compute $\operatorname{sech}(x) = 1 / \cosh(x)$ instead of acb_sech, far more bisections would have been needed just to get finite bounds $M$.
An adversarial user might try to invent a pole-free integrand that still has narrow peaks or rapid oscillations on the real line, for example using Gaussian functions $e^{-Cx^2}$. However, holomorphic functions with such behavior will always grow rapidly in the imaginary direction, and this behavior gets caught no matter what. The wonders of complex analysis! To illustrate that the algorithm works well with oscillatory functions, we can try $$\int_0^8 \sin(x + e^x) dx$$ whose graph crosses the $x$-axis some 950 times:
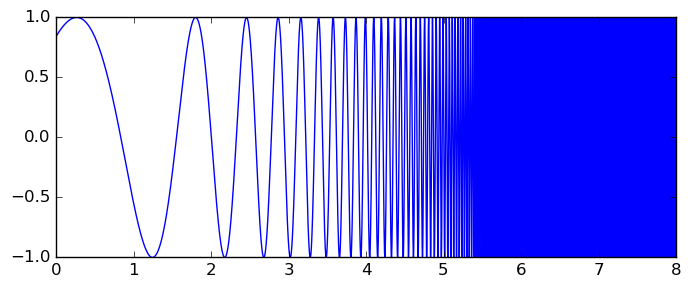
This integral was proposed as test problem in 2010 by Siegfried Rump (the author of INTLAB), who noticed that it kept MATLAB's quad function busy for over a second before returning the wildly inaccurate estimate 0.2511 without warning. It is no match for us. With 64-bit, 333-bit and 3333-bit precision, Arb takes 0.0085 seconds, 0.021 seconds and 1.2 seconds respectively, giving the results:
[0.34740017265725 +/- 3.95e-15] [0.34740017265724780787951215911989312465745625486618018388549271361674821398878532052968510434660 +/- 5.97e-96] [0.34740017265724780787951215911989312465745625486618018388549271361674821398878532052968510434660410575681379617200601870730271422819761807370400435367845286662743627947197021641090871604357741290995606858777670471094869127959300456782109150892536995724063954729888645233268526438190303909887052516007600597816880806274656413498773105014211930634630781211450442039858415941713109690079803966201822164112726627130156915990854138606297576388881321216470287266108535646432360372672288693673200846375675525487567875023485730930248989542956203963227259269550259688044756306012838422351518141678635534771338613942368836246521883930960659863728405242317701055897531410313414784141350588103328154728710306585886533927879068628857684780802416600675328289528066671518145202609909170792617267516330212201319054843192851242746577402103484375544574290645832258539603442623681567079591030149072830083221467231117502559209209775324912226134278283137642656133104212839636778216311566333263377302773070729359519475274 +/- 2.95e-999]
GL quadrature is particularly efficient for entire functions (like this one) since $\rho$ in principle can be taken arbitrarily large. The number of bisections actually decreases with the precision in this case: Arb uses 96, 39 and 8 terminal subintervals for this integral at 64, 333 and 3333 bits of precision, performing 4325, 5410 and 10417 total function evaluations. Notably, Arb computes this integral to 1000-digit accuracy faster than INTLAB computes it in machine precision interval arithmetic, while the recently published formally verified integrator in Coq takes 80 seconds to determine just one digit.
GL quadrature uses the roots of Legendre polynomials as evaluation points. Generating the necessary nodes only takes a few milliseconds at precision up to a few hundred bits and a couple of seconds at 3333-bit precision. This is an order of magnitude faster than any other available software, thanks to highly optimized new code in Arb for evaluating Legendre polynomials (this is based on joint work with Marc Mezzarobba, which we plan to detail in a forthcoming paper). A crucial detail is that Arb caches the nodes internally, so repeated integrations at the same (or lower) precision don't have this overhead. The first example integral in this post actually takes 11 seconds starting from a cold cache (2.3 seconds to precompute nodes) and the second example takes 5.3 seconds from a cold cache (4.1 seconds to precompute nodes). All the reported timings in this post are with nodes already cached. The user can optionally control the allowed quadrature degree to get a different tradeoff between precomputation time and integration speed.
Tolerances and large and small values
The user needs to provide three parameters to acb_calc_integrate to control the accuracy: the working precision (prec) in bits, the absolute tolerance $\varepsilon_{\text{abs}}$, and the relative tolerance $\varepsilon_{\text{rel}}$. Actually, $\varepsilon_{\text{abs}}$ is provided as a mag_t while $\varepsilon_{\text{rel}}$ is provided as a machine integer $g$ such that $\varepsilon_{\text{rel}} = 2^{-g}$ (this might seem inconsistent, but I conclued after a long period of deliberation that it really is most natural to specify the relative tolerance in the same way as a precision, and this makes most sense from the implementation point of view too). Given this data, the algorithm attempts to achieve an error bounded by $$\max(\varepsilon_{\text{abs}}, M \varepsilon_{\text{rel}})$$ on each subinterval, where $M$ is the magnitude of the integral. In typical scenarios (where it can be assumed that $M$ will be around unit magnitude), the user should set $\varepsilon_{\text{abs}} = \varepsilon_{\text{rel}} = 2^{-\text{prec}}$. In some scenarios, different tolerances should be used. If the user wants $g$ bits of precision but evaluating the integrand loses $m$ bits of precision due to numerical instability, the tolerances should be set to $\varepsilon_{\text{abs}} = \varepsilon_{\text{rel}} = 2^{-g}$ while the working precision should be set to $g + m$. If $M$ might differ from unity by many orders of magnitude, the user can specify a relative tolerance alone and set $\varepsilon_{\text{abs}} = 0$. This is best avoided if possible, because $M$ has to be estimated during the execution algorithm, and it can take many bisections to find the "right scale"; it will generally be more efficient to set $\varepsilon_{\text{abs}} \approx M \varepsilon_{\text{rel}}$ if an estimate for $M$ is known.
To illustrate, here is an integral with large magnitude due to a sharp peak (note that a constant factor has been taken out in the plot since Matplotlib doesn't work with large numbers): $$\int_0^{10000} x^{1000} e^{-x} dx = \gamma(1001,10000) \approx 4.0238726 \cdot 10^{2567}.$$
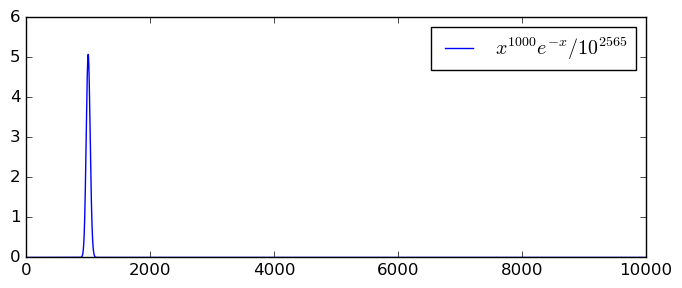
- With 64-bit precision (and 64-bit relative accuracy goal), the integration with $\varepsilon_{\text{abs}} = 0$ or $\varepsilon_{\text{abs}} = 2^{-64}$ takes 0.06 seconds, giving [4.023872600770938e+2567 +/- 8.39e+2551]. If we set $\varepsilon_{\text{abs}} = 10^{2551}$, the time drops to 0.006 seconds and the result is [4.02387260077094e+2567 +/- 3.19e+2552].
- With 333-bit precision, using either $\varepsilon_{\text{abs}} = 2^{-333}$ or $\varepsilon_{\text{abs}} = 0$ takes 0.09 seconds while setting $\varepsilon_{\text{abs}} = 10^{2467}$ reduces the time to 0.02 seconds.
- With 3333-bit precision, using either $\varepsilon_{\text{abs}} = 2^{-3333}$ or $\varepsilon_{\text{abs}} = 0$ takes 1.5 seconds while $\varepsilon_{\text{abs}} = 10^{1567}$ reduces the time to 0.6 seconds.
Conversely, consider a (very easy) integral with small magnitude: $$\int_{-1020}^{-1010} e^x dx \approx 2.304 \cdot 10^{-439}.$$
With 64-bit precision and the recommended absolute tolerance of $\varepsilon_{\text{abs}} = 2^{-64}$ acb_calc_integrate returns [+/- 2.31e-438] in 0.000001 seconds (1 microsecond), having performed just one function evaluation. With 3333-bit precision and $\varepsilon_{\text{abs}} = 2^{-3333}$, we get
[2.30437715094936344240335273034197433177002503022372248067130030654876805851618814578494982173813152038262832228300985376186030512889812686914314418932863057092655727317518452906431039449056763344722068736513538515837985119675944663784889929907823490759129662635185899863308721940993011360921101818541540011288088628857085421893956712224567570034638742275681598813382278076812454580943444313172172612797874051536134282021987084753342671324270419006870470466268509001936818680052966283104392257413838370578070824927539559165757119090411085482082755331623953811709116144626778991410155694941e-439 +/- 5.23e-1027]in 0.01 seconds. This is fine if we only care about the absolute error, but for high relative accuracy, we should set a smaller absolute tolerance.
With 64-bit precision and $\varepsilon_{\text{abs}} = 0$, it takes 0.00015 seconds and the result is [2.304377150949363e-439 +/- 5.91e-455]. With 64-bit precision and $\varepsilon_{\text{abs}} = 10^{-455}$, the time drops to 0.000028 seconds and the result is [2.304377150949363e-439 +/- 5.99e-455].
With 333-bit precision, the time with $\varepsilon_{\text{abs}} = 0$ versus $\varepsilon_{\text{abs}} = 10^{-539}$ is 0.00058 versus 0.00015 seconds; with 3333-bit precision the time for $\varepsilon_{\text{abs}} = 0$ versus $\varepsilon_{\text{abs}} = 10^{-1439}$ is 0.06 versus 0.02 seconds.
We see that an accurate estimate for the absolute error is more efficient than a pessimistic lower bound or zero. The handling of $\varepsilon_{\text{abs}} = 0$ could no doubt be optimized. Various heuristics are possible: one possibility is to do a low precision integration to estimate the magnitude before doing a higher precision integration. However, there will always be cases where automatic heuristics perform poorly, and optimal performance requires some judgement calls by the user. For these two examples, we know something about the shapes of the integrands: the magnitude of the first integral should be close to $1000^{1000} e^{-1000} \approx 10^{2566}$, and for the second integral computing the magnitude at the right endpoint is enough.
It is important to note that acb_calc_integrate does not change the working precision adaptively, and this means that the tolerances only act as guidelines and generally will not be met strictly. The final error depends on rounding errors in the evaluation of the integrand, the number of subdivisions, and cancellation between segments of the integral. This is in line with the general precision semantics in Arb, where the working precision acts as a work factor and the user is responsible for adjusting the precision on a higher level as needed. An example with cancellation is $$\int_{-10}^{10} \sin(x) + \exp(-200-x^2) dx$$ where the tiny Gaussian term is hidden behind a function that cancels out itself when integrated over the whole interval. This integration takes 0.00035 seconds with 64-bit precision, giving [+/- 2.08e-17]. It takes 0.0013 seconds with 333-bit precision, giving [2.4528927281e-87 +/- 6.56e-98].
Infinite intervals and endpoint singularities
The algorithm only converges for proper integrals. That is, the integration path must be finite, and the function must be bounded on this path. Trying to evaluate an improper integral will not give an incorrect result; the adaptive subdivision will simply proceed until the user-configurable limit on the number of evaluations or local bisections is exceeded, at which point a non-finite enclosure ($[\pm \infty] + [\pm \infty] i$) is returned. In the common situation with a blow-up singularity at an endpoint and/or an integrand that decays towards infinity, a general workaround is to compute a truncated version, say $\int_a^{\infty} f(x) dx \approx \int_{a+\varepsilon}^N f(x) dx$, and add bounds for the truncation error separately. This must be done manually. Fortunately, deriving tail bounds tends to be a manageable problem (at least for integrands given by explicit formulas), and adaptivity ensures that the truncated part of the integral can be computed numerically even if the integration path is very extended or comes very close to a singularity.
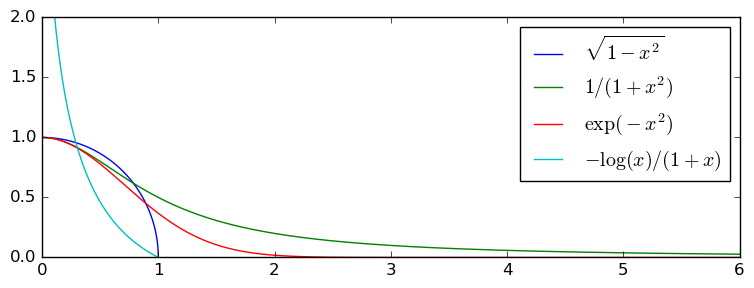
The table below compares the computation of five integrals at 64, 333 and 3333 bits of precision (the image above plots the integrands). $I_1$ is an ordinary proper integral. $I_2$ (which measures the area of the quarter-disk) is a proper integral, but the endpoint $x = 1$ is a branch point singularity that ends the region of holomorphicity. $I_3$, $I_4$ are integrals over the half real line, and need to be truncated at a finite upper limit $N$, while $I_5$ has a blow-up singularity at $x = 0$ and needs to be truncated at a nonzero lower limit $\varepsilon$. In all cases, Arb computes an accurate enclosure for the integral with radius just slightly larger than $2^{-p}$ at $p$-bit precision. These particular integrals were chosen for having the nice closed form values $4I_1 = 4I_2 = 2I_3 = 4 I_4^2 = 12 \sqrt{I_5} = \pi$, so it is easy to check the results.
| Integral | Precision | Time (seconds) | Subintervals | Evaluations |
|---|---|---|---|---|
| $$I_1 = \int_0^1 \frac{dx}{1+x^2}$$ | 64 | 0.000036 | 2 | 52 |
| 333 | 0.00019 | 2 | 188 | |
| 3333 | 0.013 | 2 | 2056 | |
| $$I_2 = \int_0^1 \sqrt{1-x^2} dx$$ | 64 | 0.00054 | 44 | 674 |
| 333 | 0.014 | 223 | 12735 | |
| 3333 | 7.4 | 2223 | 1188115 | |
| $$I_3 = \int_0^{\infty} \frac{dx}{1+x^2}$$ | 64 | 0.0020 | 191 | 2894 |
| 333 | 0.047 | 998 | 51907 | |
| 3333 | 27 | 9998 | 4711135 | |
| $$I_4 = \int_0^{\infty} e^{-x^2} dx$$ | 64 | 0.00019 | 4 | 138 |
| 333 | 0.0012 | 4 | 551 | |
| 3333 | 0.22 | 4 | 3894 | |
| $$I_5 = \int_0^1 \frac{-\log(x)}{1+x} dx$$ | 64 | 0.0033 | 189 | 2782 |
| 333 | 0.10 | 997 | 52024 | |
| 3333 | 335 | 9997 | 4720879 |
Implementing the integrals with Arb code requires just a little bit of work:
- The integrand for $I_1$ and $I_3$ has poles at $\pm i$, which are caught automatically when performing the division in complex interval arithmetic.
- In $I_2$, we must use a square root function that (unlike the standard acb_sqrt) signals non-holomorphicity when crossing the branch cut. This is easily done as shown in the example program.
- The tail of $I_3$ is bounded by $\int_N^{\infty} 1/x^2 dx = 1/N$, so we truncate at $N = 2^p$ where $p$ is the wanted number of bits, and then add $[\pm 2^{-p}]$.
- The tail of $I_4$ is bounded by $e^{-N^2}$, so we truncate at $N = \lceil \sqrt{p \log(2)} \rceil$ and add $[\pm 2^{-p}]$ (actually, the code adds $[\pm e^{-N^2}]$ since this allows choosing $N$ more simply using floats).
- For $I_5$, comparison with $\int_0^{\varepsilon} -\log(x)dx = \varepsilon (1 - \log(\varepsilon))$ shows that the error from truncating at $\varepsilon = 2^{-N}$ is bounded by $2^{-N} (1+N)$. In general, we should also check for the branch cut of the logarithm in $I_5$, but this is not needed for the integration path $[0,1]$ since any ellipse that reaches the branch cut will go through the blow-up point $x = 0$.
We can see that $I_1$ and $I_4$ are the cheapest integrals to evaluate: they only require $O(1)$ subdivisions and $O(p)$ function evaluations for $p$-bit accuracy. The running time for $I_4$ is a bit higher since the exponential function is more costly to evaluate than an arithmetic operation. $I_2$, $I_3$ and $I_5$ are categorically worse: they require $O(p)$ subdivisions and $O(p^2)$ evaluation points. The interval $[0,2^p]$ for $I_3$ needs to be subdivided into segments $[2^k, 2^{k+1}]$, while successive subdivisions into segments of width $2^{-k}$ are needed near the singularities of $I_2$ and $I_5$. Qualitatively, this happens because the singularities (the point at infinity counts as a singularity) are of a "slow" type, i.e. algebraic or logarithmic. Since the singularity at infinity in $I_4$ is approached at an exponential rate, the same amount of splitting is not needed.
$O(p^2)$ evaluations is an acceptable complexity for arbitrary-precision computation, but it is not optimal. With a bit of preprocessing, we can actually improve convergence very substantially for many integrals with algebraic or logarithmic singularities: we simply make a suitable exponential change of variables to change the rate of approach. For example, we can make the substitutions $x \to \tanh(x)$ in $I_2$, $x \to \sinh(x)$ in $I_3$, and $x \to e^{-x}$ in $I_5$. Simplifying the resulting expressions gives the following equivalent integrals with exponential decay on $[0,\infty)$ (for which one easily finds good truncation points $N$).
| Integral | Precision | Time (seconds) | Subintervals | Evaluations |
|---|---|---|---|---|
| $$I_2 = \int_0^{\infty} \operatorname{sech}^3(x) dx$$ | 64 | 0.00038 | 10 | 257 |
| 333 | 0.0031 | 12 | 1174 | |
| 3333 | 0.83 | 14 | 13499 | |
| $$I_3 = \int_0^{\infty} \operatorname{sech}(x) dx$$ | 64 | 0.00031 | 10 | 249 |
| 333 | 0.0030 | 14 | 1298 | |
| 3333 | 0.96 | 17 | 16585 | |
| $$I_5 = \int_0^{\infty} \frac{x e^{-x}}{1 + e^{-x}} dx$$ | 64 | 0.00025 | 8 | 207 |
| 333 | 0.0028 | 10 | 994 | |
| 3333 | 0.82 | 14 | 14097 |
The convergence is now essentially as rapid as possible. A natural question arises: could the integration algorithm apply such transformations automatically? The answer is "almost". In fact, this is part of the idea behind the the double exponential method. However, if one wants to bound the error rigorously, this requires some "global" symbolic information about the integrand beyond black-box evaluation for local values. Such global information might consist of a bound of the type $|f(x+yi)| \le C x^{\alpha}$ for all $x > N$ for a slowly decaying integrand on $[0,\infty)$, for example. Semi-automatic support for some reasonably nice classes of improper integrals where such information can be provided by the user should be possible in the future.
Too much oscillation
We can cope with oscillatory functions (as long as the number of oscillations is bounded) and functions that decay smoothly, but oscillatory functions with slow decay on an infinite interval are a lethal cocktail for any general-purpose integration algorithm. While an integral like $\int_0^{\infty} e^{-x} \sin(x) dx$ poses no problem due to the exponential decay, an integral like $\int_1^{\infty} \sin(x) / x^2 \, dx$ is problematic. Without essentially changing the problem, we can invert the variable so that the oscillations have a finite accumulation point, say at $x = 0$ (just for demonstration purposes). From the complex point of view, this makes $x = 0$ an essential singularity. Consider these two examples: $$I_1 = \int_0^1 \sin(1/x) dx \quad \left(= \int_1^{\infty} \frac{\sin(x)}{x^2} dx\right)$$ $$I_2 = \int_0^1 x \sin(1/x) dx \quad \left(= \int_1^{\infty} \frac{\sin(x)}{x^3} dx\right) $$ Here are both functions visualized:
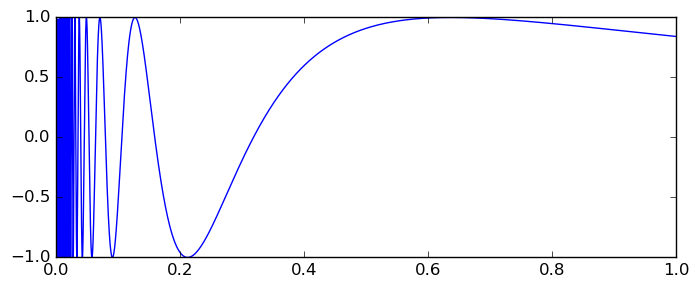
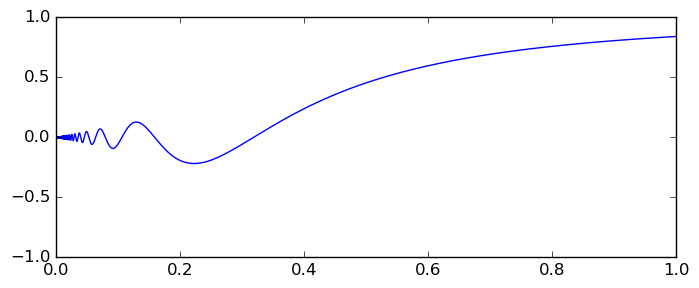
If we attempt to compute either integral using 64-bit precision with default options, acb_calc_integrate aborts after 0.2 seconds and returns $I_1 =$ [+/- 1.27], $I_2 =$ [+/- 1.12]. This seems too pessimistic. What happened here? The explanation is a bit technical. Internally, the integration code needs to maintain a queue of unfinished subintervals. The integration converges when satisfactory accuracy is reached on all subintervals, and when this happens, the order of the queue is largely irrelevant. However, if the limit on the number of function evaluations or subintervals is exceeded (which happens when convergence is too slow, as in this case), the algorithm stops doing further bisections, and in this case the results can be sensitive to the order of the queue.
By default, the integration code uses an "greedy" subdivision strategy, in which the queue works as a stack. If the subinterval at the top of the queue needs to be bisected, the code simply adds both the new sub-subintervals at the top of the queue (with the one with the larger estimated error on top). In this case, this leads the algorithm to focus on the difficult subintervals near $x = 0$ while the easy interval $[0.5,1]$ remains at the bottom of the queue the whole time! The user can avoid this problem in two different ways:
- Reduce the accuracy goal so that the integration near $x = 0$ converges.
- Toggle the use_heap option, which makes the integration code use a sorted max heap for the queue so that the subinterval with the largest error globally always gets the highest priority.
Specifying an absolute tolerance of $10^{-6}$ gives the following results (in 0.01 seconds for the first integral and 0.0008 seconds for the second):
[0.504 +/- 2.68e-4] [0.37853 +/- 6.35e-6]
With use_heap, we get (in 0.007 seconds for the first integral and 0.01 seconds for the second):
[0.504 +/- 7.88e-4] [0.3785300 +/- 3.17e-8]
The reader might wonder why use_heap is not the default. While this improves results when isolated problematic points "steal the attention" of the subdivision algorithm and prevent convergence, it requires a far larger queue when many bisections are needed globally. The default greedy strategy is more efficient and robust for integrals that require many subdivisions but ultimately do converge, which is the more interesting case in general. With that said, it should be possible to implement some more intelligent heuristic in the future to get the best of both worlds.
It's possible to compute a few more digits. We get the following results in 17 seconds with use_heap if we increase the limit on function evaluations and subintervals to $10^7$:
[0.504067 +/- 2.78e-7] [0.3785300171242 +/- 5.75e-14]
High accuracy is out of reach on such examples without using specialized algorithms for oscillatory integrals. For comparison, scipy.integrate.quad returns 0.5024347 for the first integral along with a slightly too optimistic error estimate 0.00062 (but it does give a warning), and mpmath.quad with default precision returns 0.5055192 (with the error estimate 0.01). These integrals can however be computed to (heuristic) high accuracy using mpmath.quadosc:
>>> mp.dps = 30 >>> quadosc(lambda x: sin(x)/x**2, [1,inf], omega=1) 0.504067061906928371989856117741 >>> quadosc(lambda x: sin(x)/x**3, [1,inf], omega=1) 0.378530017124161309881735275628
I have not yet thought about how to make such methods rigorous.
Special functions
Integration works out of the box with all the special functions implemented for complex variables in Arb. There is a caveat: many function implementations are not yet designed to give reasonable enclosures for the wide input intervals needed to determine the quadrature error bounds, so the user might have to implement a custom evaluation strategy for such input in order to get good performance. The user also needs to know about branch cuts, where applicable. As two quick examples, one integral of the principal branch of the Lambert W function on the real line (the code checks for the branch cut to ensure correctness) and one of the gamma function on a vertical line in the complex plane:
| Integral | Precision | Time (seconds) | Subintervals | Evaluations |
|---|---|---|---|---|
| $$\int_0^{1000} W_0(x) dx$$ | 64 | 0.00081 | 12 | 273 |
| 333 | 0.0092 | 12 | 1109 | |
| 3333 | 1.3 | 12 | 12043 | |
| $$\int_1^{1+1000i} \Gamma(x) dx$$ | 64 | 0.023 | 64 | 1524 |
| 333 | 0.46 | 69 | 6502 | |
| 3333 | 225 | 72 | 73423 |
Here, the evaluation of bounds for the gamma function near $x = 1$ causes slowdown (see this previous post) and fixing it would save a factor two.
For reference, the 3333-bit results are (for the Lambert W integral)
[4439.093452951029884267853905009737305420193885706648763311802561502510792049833842664821873546398606801868264189207356150953363442753390866898448548988757721792146768252974409964536413679904629270555468530438573165148921358413890143571915238783080913081011481879388664963500773837154421564769922676845276569849543495375165685478676203295634185489766099113920822045116924255649326008340685395370223624978986009592070090218963365043486328957171927380836891972378262054880688518399229428757005459949632460284771969645521419356281013295316046561396028993671141780952241874764111095828789354907786052371361080373372009159323384226199578698768128109276792600905791838387591363703307640036732208612087841146272201415978429929488488686114363445415965303620737561198957585068037333612385255515795437920578608940741395966830398511498480093830918358905297086025859463952416764440794250671774382855247814010923571013850424507537211014515743403487717704098043192914950399963356994781532580872519136869288866731381 +/- 5.58e-997]and (for the gamma integral)
[0.154479641320042744690188534802211028377383691851677508919090688295930859289429184352803659448703345658903547755842803079249535972772848198865241428093549171776340634242451462951513409158019496873808314878181533915490287792649738793204165555018328176591534971452713507884748971852047603753886670175478355027329954979909582954908097045750201937151894873543074176797230020754116175162874153747159968973528327311669521172018384139733245219461522260527522520794813361937933368623134728577018752202066446077045103736358928601032859283859190261473992283107452936804466455121350317183749936985962194931624140006229709905896530975157558516623849945263658691485382524479354908100442531093784034712396156463465459911219494893649512047988021348350277406736326810929397963193665265086492779227909925131026077802376402168614298032073407796380949086083173337524414746363926680175211343133895805165991586269381775720598824920169216850738248802938219708563156638389273660792179772817116245557878427767342428224543 +/- 4.30e-997] + [1.155727349790921717910093183312696299120851023164415820499706535327288631840916939440188434235673558804486653687020700914219048007856360834437788613604544109645138219699555760622688895095637708058521986351218058537072313555659213333540958073313072832258994713597286225874168717495150020490242380114361210253354248005121620381707436457581844477849073133292563066824375117397039091655480858601593812646976505626483014738577409093957259348879038526548445285181544302974337749467175663680215389822335712510537929376659437163313300972259335901914385137815906346297332730048394341125224742228356033426229396672714052611764897300694648779797881260377819399291544852948162579800091671694879260504634350639720853933239367015763358430960029829821479543050609001169879253993965166893478944293777262045728373793077865379599837062408310959498876677101978246957327147594693995351121733684997398941122198172062879848146014134641773605697876027327225078050917411810935179929773659029121386034609909881705794720053 +/- 3.21e-997]*I
A nice application of contour integration is computing derivatives, or more generally coefficients in Laurent expansions. Consider the Weierstrass elliptic function, implemented in Arb as acb_elliptic_p. It has a Laurent series $$\wp(z; \tau) = \sum_{n=-2}^{\infty} a_n(\tau) z^n$$ at the origin. We can compute the Laurent coefficients using the Cauchy integral formula $$a_n = \frac{1}{2\pi i} \int_\gamma \frac{\wp(z)}{z^{n+1}} dz$$ where the path $\gamma$ circles the origin counterclockwise without going around any other lattice points. We pick the lattice $\tau = i$ and use the path consisting of four rectilinear line segments connecting the corners $0.5-0.5i, 0.5+0.5i$, etc. At 333-bit precision, the coefficients up to $n = 100$ computed this way are:
a[-2] = [1.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 +/- 3.57e-98] + [+/- 1.89e-98]*I a[-1] = [+/- 4.11e-98] + [+/- 2.57e-98]*I a[0] = [+/- 1.02e-97] + [+/- 5.39e-98]*I a[1] = [+/- 1.41e-97] + [+/- 1.35e-97]*I a[2] = [9.453636006461692614653069826746065669936558063544557315411621072152779513048238364832608318652235 +/- 4.44e-97] + [+/- 2.48e-97]*I a[3] = [+/- 4.47e-97] + [+/- 4.60e-97]*I a[4] = [+/- 8.65e-97] + [+/- 8.04e-97]*I a[5] = [+/- 1.58e-96] + [+/- 1.58e-96]*I a[6] = [29.79041124755632662913008276518092149986728354527080122957000856565595849647256804092821881306410 +/- 7.87e-96] + [+/- 2.95e-96]*I a[7] = [+/- 5.47e-96] + [+/- 5.54e-96]*I a[8] = [+/- 1.12e-95] + [+/- 1.09e-95]*I ... a[94] = [380.000000000001350031197944195149614241959414332513607395378210489263746 +/- 9.24e-70] + [+/- 8.27e-70]*I a[95] = [+/- 1.37e-69] + [+/- 1.37e-69]*I a[96] = [+/- 2.93e-69] + [+/- 2.91e-69]*I a[97] = [+/- 5.81e-69] + [+/- 5.82e-69]*I a[98] = [395.9999999999996482813457987507203762431512516114852024749894232346383 +/- 2.90e-68] + [+/- 1.17e-68]*I a[99] = [+/- 2.32e-68] + [+/- 2.32e-68]*I a[100] = [+/- 4.95e-68] + [+/- 4.95e-68]*I
The coefficients with odd $n$ are always zero, and we see that the coefficients with $n \equiv 0 \bmod 4$ are zero for this lattice also. The time increases quite slowly when $n$ grows: $a_{-2}$ takes 0.67 seconds and $a_{100}$ takes 0.85 seconds. On each of the four segments, the number of used subintervals is of the order 20-50 and the number of function evaluations is 2000-8000 at this precision. At 64-bit precision, the time is around 0.05 seconds per coefficient, and at 3333-bit precision, the time is around 120 seconds. There is some cancellation of the order of $n$ bits with this contour. The plot below shows the real and imaginary parts of $\wp(z; \tau) / z^{100}$ for $z = 0.5+xi$ (note the vertical scale):
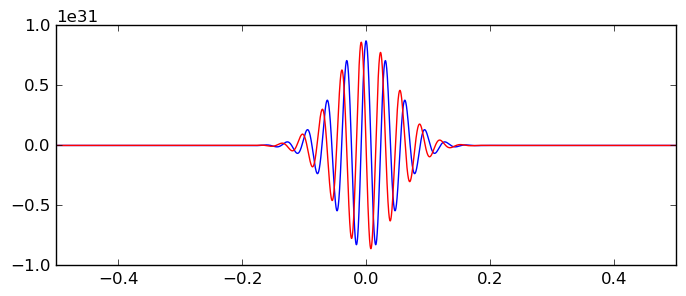
A much faster way to compute these coefficients is to use the function acb_modular_eisenstein, but here the idea is of course to demonstrate the principle of numerical integration.
Another nice application of contour integration is to count zeros and poles of analytic functions. How many zeros $\zeta(\rho_n) = 0$ does the Riemann zeta function have on $R = [0,1] + [0,T] i$? The argument principle tells us that $$N(T) = 1 + \frac{1}{2 \pi i} \int_{\gamma} \frac{\zeta'(s)}{\zeta(s)} ds$$ where $\gamma$ traces the boundary of $[-\varepsilon, 1+\varepsilon] + [0,T] i$ (plus a small excursion to include the pole at $s = 1$, which accounts for the "1+" term). A more numerically useful version of this formula can be derived using the functional equation of the Riemann zeta function, giving $$N(T) = 1 + \frac{\theta(T)}{\pi} + \frac{1}{\pi} \operatorname{Im} \left[ \int_{1+\varepsilon}^{1+\varepsilon+T i} \frac{\zeta'(s)}{\zeta(s)} ds + \int_{1+\varepsilon+T i}^{\tfrac{1}{2} + T i} \frac{\zeta'(s)}{\zeta(s)} ds \right]$$ where $\theta(T)$ is the Hardy theta function. We set $\varepsilon = 99$ (!) so that the first integral becomes easy to evaluate. Using a tolerance of $10^{-6}$ for the integration (since we only need to determine $N(T)$ to the nearest integer), 32-bit working precision for $T \le 10^6$ and slightly higher 48-bit precision for $T = 10^7, 10^8, 10^9$, we obtain the following values:
| $T$ | Time (seconds) | Evaluations | Subintervals | $N(T)$ |
|---|---|---|---|---|
| 100 | 0.044 | 261 | 24 | [29.00000 +/- 1.94e-6] |
| $10^3$ | 0.51 | 1219 | 109 | [649.00000 +/- 7.78e-6] |
| $10^4$ | 13 | 6901 | 621 | [10142.0000 +/- 4.25e-5] |
| $10^5$ | 12 | 4088 | 353 | [138069.000 +/- 3.10e-4] |
| $10^6$ | 16 | 5326 | 440 | [1747146.00 +/- 4.06e-3] |
| $10^7$ | 42 | 4500 | 391 | [21136125.0000 +/- 5.53e-5] |
| $10^8$ | 210 | 6205 | 533 | [248008025.0000 +/- 8.09e-5] |
| $10^9$ | 1590 | 8070 | 677 | [2846548032.000 +/- 1.95e-4] |
One can cross-check with other software that $$\rho_{2846548032} \approx 0.5 + 999999999.73397 i$$ $$\rho_{2846548033} \approx 0.5 + 1000000000.11565 i$$ so the results really are correct. Higher precision is of course also possible (though unnecessary for this application). For example, with 333-bit precision, it takes 33 seconds to compute $N(1000)$ as:
[649.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 +/- 3.56e-97]
The irregular dependence on $T$ in the timings is due to suboptimal cutoffs between Euler-Maclaurin summation and the Riemann-Siegel formula to compute $(\zeta(s), \zeta'(s))$ off the critical line. With fine-tuning, I believe the time could be reduced quite a bit further. I was actually surprised to see that brute force numerical integration scales this well. Of course, this is not the best way to compute $N(T)$; using Turing's method (not yet implemented in Arb), which only needs a handful of evaluations of the Riemann zeta function on the critical line, $N(10^9)$ could be computed in a fraction of a second.
Discontinuities
The combination of adaptive subdivision and local GL quadrature provides fast convergence for piecewise holomorphic functions. As a special case, it provides fast convergence for functions on $\mathbb{R}$ with isolated discontinuities or derivative discontinuities, provided that the smooth parts have local holomorphic extensions. For example, this works for functions containing $\lfloor f(x) \rfloor$ or $|f(x)|$ where $f$ is a real analytic function with a holomorphic extension, as shown in the example program:
- The floor function on $\mathbb{R}$ can be extended to a piecewise holomorphic function equal to the constant function $n$ on the strip $\operatorname{Re}(z) \in [n, n+1)$.
- The absolute value function is not holomorphic on $\mathbb{C}$, but we can extend its restriction to $\mathbb{R}$ to a piecewise holomorphic function essentially by defining it as $|z| = \sqrt{z^2}$ which is equal to $z$ in the right half plane and $-z$ in the left half plane, with branch cuts on $(-i\infty,0]$ and $[0,i\infty)$.
Harald Helfgott asked about rigorous computation of integrals such as the following in a question on MathOverflow in 2013:
$$\int_0^1 |(x^4 + 10x^3 + 19x^2 - 6x - 6) \, \exp(x)| \, dx$$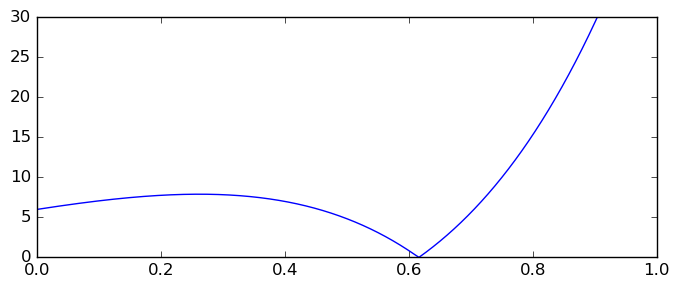
I'm using this example after having seen it in a talk by Guillaume Melquiond about formally verified integration in Coq last year. Not only does this innocent-looking function confuse MATLAB's quad and quadgk routines into returning results with unexpectedly low accuracy (only 10 correct digits); until 2016, the interval software INTLAB computed an incorrect enclosure for this integral! No software is immune to bugs! (Well, certain software written in Coq might be.) Arb, at least, computes this integral correctly, giving the following enclosures at 64, 333 and 3333 bits of precision:
[11.1473105500571397 +/- 5.42e-17] [11.147310550057139733915902084255301415775813549800589418261584268232061665808482234384871404010464 +/- 2.28e-97] [11.14731055005713973391590208425530141577581354980058941826158426823206166580848223438487140401046397082620181479808745215150214966606117998798072737731641405804570978139538371330820522555080766169854758454942405170903216151250601358070566105756770607003825904144018310923829606165174603691357807682566856414814440582958156624560187687359243481200598216391218817315280020901199979652701634362305831291093522299734696647030916641843175954876732333011065844446103832308221764075622012831031601468915704497249435860755470750474329770257187337837407957279254795614325730321024917557423879650360200306171040482068651669142274175163594700441390155104322881415469832145730706663467647531892559459341400694664132517564554130114751424081973706457060160886895543090755477147097016502491484468485766698656347906525894833136667919722152390015744673677703468657201968292052223937911432100019672280145364825194158075081632814785795604352662947745666313275560182281201678530658430829694436463131676725074258868025617 +/- 4.81e-999]
The time is 0.0015, 0.052 and 108 seconds, using 1093, 18137 and 1624951 function evaluations and 70, 339 and 3339 terminal subintervals. The amount of work grows like $O(p^2)$, as one would expect since it takes $O(p)$ bisections to chase down the branch point to a negligible interval. A much more efficient method would be to locate the root of the expression passed to the absolute value and split the integration into two segments with fully branch cut-free integrands, but the naive method does work without any hassles. As a small optimization, I did move the exponential out of the absolute value in the code, to avoid evaluating it when it will not be needed.
There is a famous but likely apocryphal story that Gauss as a young schoolboy calculated the sum $1 + 2 + 3 + \ldots + 99 + 100$ in a few seconds (to the astonishment of his teacher) by pairing the terms to obtain $50 \times (100 + 1) = 5050$. We can compute this sum in a much more roundabout way by posing it as the integral $$\sum_{n=1}^{100} n = \int_1^{101} \lfloor x \rfloor dx.$$
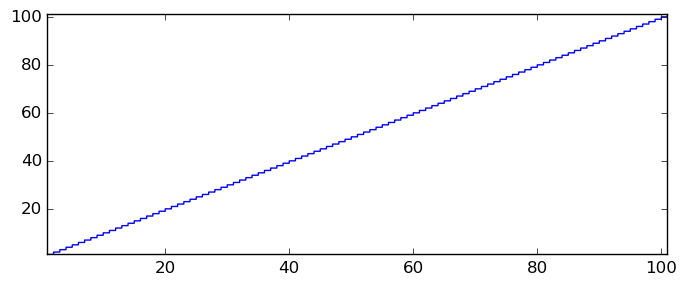
Arb computes the following enclosures:
[5050.000000000000 +/- 2.67e-13] [5050.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 +/- 2.83e-94] [5050.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 +/- 2.30e-997]
The time is 0.014, 0.11 and 1.5 seconds, using 16606, 100534 and 443889 function evaluations and 5536, 33512 and 345512 terminal subintervals. Just as one would expect, we end up on about $100p$ subintervals when trying to locate the 100 discontinuities to $p$-bit precision by bisection. Obviously, for a piecewise constant function, trying to use GL quadrature on each subinterval is a waste of time, and if we disable it, the time drops by about half. This is an extremely silly example, but we can also consider less trivial discontinuous functions. Let us revisit Rump's example, but this time we butcher the integrand:
$$\int_0^8 \left(e^x - \lfloor e^x \rfloor \right) \sin(x + e^x) dx$$
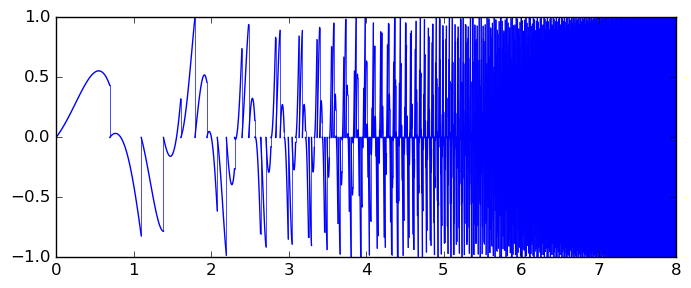
This domain coloring plot shows the piecewise holomorphic extension:

With 64-bit precision, acb_calc_integrate aborts and outputs [+/- 7.32e+3] after 0.18 seconds due to exceeding the default limit on the number of function evaluations. If we increase the evaluation limit, it finishes after 9.1 seconds and gives:
[0.0986517044784 +/- 4.37e-14]
With 333-bit precision (and increased evaluation limit), it takes 548 seconds and gives:
[0.0986517044783652061196582497648598565041696207923844914510919068308266804822906098396240645824 +/- 5.99e-95]
We could, once again, compute this integral much more efficiently by locating all the discontinuities (here found at $\log(n)$, $n = 2,3,\ldots,2980$) and taking out the floor function, but the brute force approach works well enough, at least for modest precision.
A limitation of the algorithm is that it does not permit computing high-precision enclosures for integrals of the form $\int_a^b |f(z)| dz$ where $f$ is a complex function. Such integrals can be computed using direct interval enclosures, but since GL quadrature cannot be used, one needs $O(2^p)$ evaluations for a tolerance of $2^{-p}$. A general solution is to find a decomposition $f(z) = g(z) + h(z) i$ where $g$ and $h$ are real-valued on $[a,b]$ (with piecewise holomorphic extensions). One can then integrate $\int_a^b \sqrt{g(z)^2 + h(z)^2} dz$. Finding convenient representations for $g$ and $h$ can be difficult, but a possible approach is to compute a Taylor approximation $f(z) \approx f_N(z)$ with error $\varepsilon$, extract the real and imaginary parts of the coefficients of the polynomial $f_N = g_N + h_N i$, and compute $\int_a^b \sqrt{g_N(z)^2 + h_N(z)^2} dz + |b-a| [\pm \varepsilon]$. The interval $[a,b]$ might need to be subdivided to ensure convergence and numerical stability of the Taylor series. Preliminary experiments suggest that this method is practical. In a future version, this process could potentially be automated.
What's next
The integration code is not perfect, and further testing will certainly reveal that tweaks are needed, but it seems good enough already for doing serious work. I'm interested in feedback and potential applications (one use I have in mind right now is computation of various special functions via integral representations).I'm planning to release the next version of Arb very soon (maybe within the next one or two weeks). There are some other new features that I will have to write about at another time.
fredrikj.net |
Blog index |
RSS feed |
Follow me on Mastodon |
Become a sponsor