fredrikj.net / blog /

A grimoire of functions

May 31, 2019

I'm the kind of person who reads encyclopedias front to back just for fun, and I've been fascinated by mathematical special functions at least since my first encounter with the gamma function as a teenager. My work implementing numerical and symbolic algorithms in mpmath, Arb and other software projects during the last 10+ years has required digging deep through the mathematical literature for useful special function identities and also deriving a few new formulas of my own. It should come as no surprise that this work has made me conscious of the limitations of the tools I'm using. I've increasingly come to think that there are two big problems that someone really ought to address:

  1. The available mathematical reference works are not good enough.
  2. The available computer algebra systems are not good enough.
By good enough, I mean good enough for my personal needs, of course -- other people have different tastes and requirements. Anyway, earlier this year, I finally asked myself seriously: why don't I just fix both problems myself? In a stroke of laziness, impatience and hubris, I celebrated Pi Day (March 14) by starting... drumroll... Fungrim: the Mathematical Functions Grimoire!

Two and a half months later, Fungrim is still "pre-alpha", meaning that you shouldn't start depending on it yet, but it's approaching a state where I can show it to people it without feeling too embarrassed. I gave a first talk about Fungrim at a workshop in Lyon last week (slides here), and I may as well follow that up with a public blog post now.

Fungrim at a glance

What and why is Fungrim? The word grimoire means book of magic formulas. Fungrim is just that: a collection of formulas for special functions, much like the classic Abramowitz and Stegun, its modern successor the NIST Digital Library of Mathematical Functions, the Wolfram Functions Site, and many other works both analog and digital. I will explain in a moment why all those reference works aren't quite cutting it (for me), but let's first take a concrete and simple example: Euler's formula

$${e}^{i z} = \cos\!\left(z\right) + i \sin\!\left(z\right).$$

Discovered around 1740 by the Swiss Sorcerer Supreme, Leonhard Euler, this formula can transmute exponentials into trigonometric functions and vice versa. A magic formula indeed! This formula is entry e103e7 in Fungrim, one of ~1200 entries added to Fungrim so far. It is listed along with many other exponential-related entries on the Exponential function topic page. Here is a screenshot of the entry as it appears on that page:

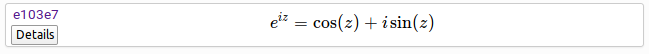
Here is a screenshot of the entry as it appears after clicking the "Details" button:

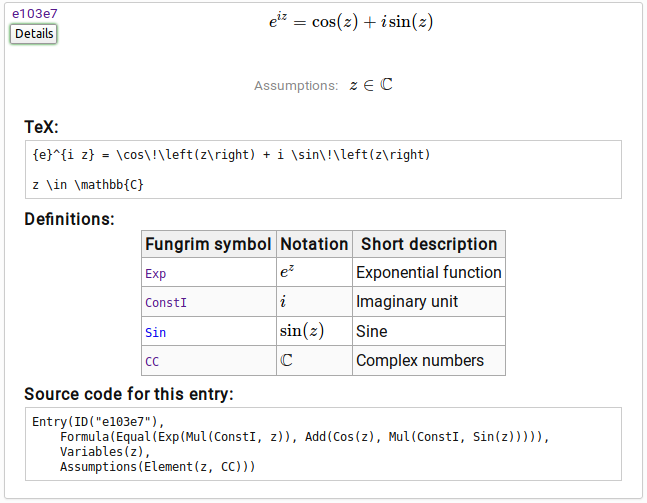
That is the essence of it! I will attempt to explain the features in more depth below.

Layout

Fungrim is designed to be clean, fast and easy to browse, both on desktops and mobile devices, and I'm pretty happy with the results so far. It still needs some touchups and usability tweaks and no doubt a lot of bugfixes for different devices and browsers that I haven't tested on myself. I'm not a real web designer or web developer, so bear with me on this!

Entry IDs

The permanent, short IDs for entries are an important feature. I can easily reference "Fungrim e103e7" (or the URL http://fungrim.org/entry/e103e7/) when I'm using this formula in some other work, much like I can reference OEIS A000041 for example. Each ID is a randomly generated hex string because I would lose sleep if I had to think about naming formulas or putting them in sequential order.

Semantic representation

Fungrim entries are not stored as TeX internally, but as S-expressions (printed as f(a, b) instead of (f a b) since I mostly work with Python, not Lisp). Unlike TeX, this representation is fully semantic; each symbol in the S-expression has a precise mathematical interpretation, and the formula is easy to manipulate algorithmically and translate into other computer algebra languages, programming languages, markup languages, etc. Functionality to export formulas to different formats directly on the website might be added in the future.

The semantic representation is not only much better than TeX for the backend processing; the user can also inspect the source code to understand the precise intent when standard mathematical notation is ambiguous. For example, the juxtaposition in $A(B+C)$ could signify either a multiplication or a function call. In the Fungrim source form, the former would be Mul(A, Add(B, C)) and the latter would be A(Add(B, C)), with no ambiguity.

The automatically-generated and hyperlinked table of definitions further allows the user to look up symbols that might be unfamiliar. This is also a goood way to discover other formulas in Fungrim featuring the same mathematical objects. You may notice that $\sin(z)$ appears in the table while $\cos(z)$ is missing -- this is because I haven't gotten around to putting in definitions for $\cos(z)$ in Fungrim yet. You can see just how much of a work in progress this is!

TeX rendering

Regardless of the internal representation, it's important to present a beautifully rendered formula to the user. This is currently achieved by converting the Fungrim code to TeX and rendering it to static HTML on the server side using KaTeX. Thanks to the server-side rendering, a page with 100 entries loads nearly instantly, which is a big step up from watching the paint dry pixel by pixel with browser-side MathJax. The only remaining problem is that the pre-rendered HTML takes up a ton of server space and bandwidth but this is not a blocker for the time being (we will see if/when Fungrim has 10-100 times more formulas and gets some real traffic).

The TeX code is displayed prominently in the detailed view, ready to copy and paste into papers, beamer presentations, etc. As I said, laziness was an important motivation for this project, and constantly retyping formulas in TeX is one of those things that annoy me as a lazy mathematician. The TeX code could be cleaned up a bit, but it's not a big deal; what matters is that the rendered formula looks great.

Assumptions

The entry includes the statement "Assumptions: $z \in \mathbb{C}$", which means that the formula is valid when any complex number is substituted for the variable $z$. In other words, the entry represents the theorem $$\forall z \in \mathbb{C}: {e}^{i z} = \cos\!\left(z\right) + i \sin\!\left(z\right),$$ just printed a little less formally. Even more precisely, the constants appearing in this entry (the functions Exp, Mul, Add, Cos, Sin, the number ConstI, and the set CC) have a fixed definition throughout Fungrim, and the formal interpretation of this entry is that the equality holds when any value of the free variable z satisfying the assumptions is substituted recursively through the S-expression (more on this below). You can find lots of formulas in Fungrim with more complicated conditions on the variables. For example, entry 7954ad gives the formula $$\operatorname{atan}\!\left(z\right) = \operatorname{asin}\!\left(\frac{z}{\sqrt{1 + {z}^{2}}}\right)$$ expressing the inverse tangent in terms of the inverse sine; the stated assumptions are $$z \in \mathbb{C} \,\mathbin{\operatorname{and}}\, i z \notin \left(-\infty, -1\right] \cup \left[1, \infty\right)$$ because the equality does not hold on the branch cuts. A rather cute entry is e6ff64 which states that $$\operatorname{Re}\!\left(\rho_{n}\right) = \frac{1}{2}$$ where $\rho_{n}$ represents a nontrivial zero of the Riemann zeta function. The assumptions are $$n \in \mathbb{Z} \,\mathbin{\operatorname{and}}\, n \ne 0 \,\mathbin{\operatorname{and}}\, \left(\left|n\right| \lt 103800788359 \,\mathbin{\operatorname{or}}\, \operatorname{RiemannHypothesis}\right).$$ The first conditions just specify the domain of definition for $\rho_{n}$; the upper bound on $|n|$ indicates the range where the formula has been shown to hold (thanks to the explicit computations done by Dave Platt). The special symbol RiemannHypothesis represents the (assumed truth of the) Riemann hypothesis. This symbol is handy for number theory estimates conditional on RH. It appears, for example, in entry 375afe which is Schoenfeld's explicit conditional bound for the prime counting function $$\left|\pi\!\left(x\right) - \operatorname{li}\!\left(x\right)\right| \lt \frac{\sqrt{x} \log\!\left(x\right)}{8 \pi}.$$ The assumptions for this entry are $$x \in \mathbb{R} \,\mathbin{\operatorname{and}}\, x \ge 2657 \,\mathbin{\operatorname{and}}\, \operatorname{RiemannHypothesis}.$$ (Here an upper bound on $x$ derived from explicit computations could be added too, but I did not look up such bounds when I added the entry.)

More on semantics

The semantic representation with strict use of assumptions is a fundamental design point which needs to be reiterated. All formula entries in Fungrim are intended to obey the following principles:

  1. All free variables are quantified, with predicates that unambiguously specify the base sets.
  2. Globally-defined functions and constants have a fixed (and consistent) meaning.
  3. Variable substitution corresponds exactly to function evaluation (or partial evaluation).

The mathematical literature is often frustrating to read simply because these principles are not followed. This means that I as a reader may have to verify the conditions and possibly fill in some gaps manually, which can add up to a huge amount of work (and potential for errors). I'm not pointing fingers here, because my own papers are among the worst offenders of all! But it's an avoidable problem. I will elaborate a bit on each point:

Point 1: it is common practice in mathematical writing to omit information about variables. This is often done for a good reason (not bogging down the text with extraneous detail), but can also be a symptom of sloppiness. Unfortunately, the outcome is that the reader sometimes doesn't have enough information to understand the content. If I come across the formula $f(n,x) = g(n,x)$ without further details, how do I know if $x$ meant to be a positive real number, a rational number, or a complex number (etc.)? Is $n$ any integer, or just a nonnegative integer, or some sufficiently large integer? Can I even be sure that $n$ represents an integer just because it's called $n$? If it's stated that $x > 0$, can I really assume that the formula holds for any positive real $x$, or is $x$ actually meant to be a positive integer? The list of potential stumbling blocks goes on. For example, $n$ might have been defined several pages earlier in the same text as a positive integer, but do I know that this is supposed to be the same $n$? (Ah, the joys of implicit context and mutable state.) Brevity is often a good thing in writing, but for a reference work, I think precision needs to be the goal.

Point 2: the literature for special functions contains many different conventions for limiting cases, branch cuts, normalizing factors, complex extensions, and so forth. Sometimes the meaning even changes within the same work! Unfortunately, it's not possible to be consistent with the rest of the world, but it's at least possible to be self-consistent. Constant symbols like CC and Pow in Fungrim are intended to represent objects in a fixed mathematical universe, with an immutable meaning. In particular, functions in Fungrim are (partial) functions on this mathematical universe, and they are meant to be functions in the formal mathematical sense. Fungrim will make an opinionated choice and stick to it consistently; for example:

These meanings cannot be overriden with handwaving alone. It's of course also possible to have alternative functions with different branch cuts and true multivalued functions that return sets or some objects representing equivalence classes, but such functions need to be formalized explicitly.

Point 3: the idea here is that S-expressions should form functions of their free variables in the obvious way, so that formulas can be evaluated and composed mechanically. Often in mathematical writing, we take a formula to define a function "modulo exceptional cases", with the understanding that the reader can fill in the gaps as needed.

For example, consider the function $f(z)$ represented by the expression $z / z$, or Div(z, z). What is the value of $f(0)$? An experienced complex analyst might remove the removable singularity without hesitation and answer that $f(0) = 1$, but this is not a valid application of variable substitution because $0 / 0$ is undefined (in Fungrim). Evaluating $f(0) = 1$ requires computing a limit, which is a more high-level manipulation than expression-level substitution. The formula $z / z = 1$ would therefore not represent a correct theorem with the assumption that $z \in \mathbb{C}$, but it would be correct with the assumption that $z \in \mathbb{C} \setminus \{0\}$. Alternatively, to get a bit technical, $z / z = 1$ would be correct with $z$ as a suitable function field or formal power series generator, say $z = x$ where $x$ is the generator of $\mathbb{C}[[x]]$, but then evaluating this "in-universe symbol" $x$ at a complex number would be a higher-level manipulation and not a valid application of expression-level substitution. As human mathematicians, we are used to doing such manipulations implicitly, but more strictly they need to be formalized explicitly (and indeed, the Fungrim formula language should allow doing so). Computer algebra systems also tend to switch between these interpretations implicitly, which is a source of bugs.

For another example, consider the equation $0^z = 0$. This is not valid (in Fungrim) without proper assumptions on $z$ because it would be inconsistent with the case $0^0 = 1$ mentioned above.

These simple examples are perhaps not convincing because it's easy to spot the exceptional cases, but life gets harder when you start composing formulas and dealing with functions of several variables! Here is a less trivial example of an inconsistency in Mathematica (and also the Wolfram Functions Site): is the confluent hypergeometric function ${}_1F_1(-1,-1,x)$ equal to $1+x$ or is it equal to $e^x$? Mathematica has a different answer depending on the variable substitution order:

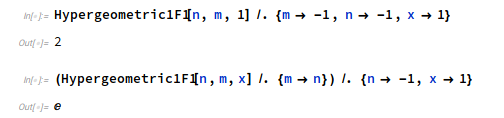
SymPy gives the same contradictory output. Depending on your point of view, this is either a violation of point 2 (self-consistent function definitions) or point 3 (consistent meaning of variable substitution). What does Fungrim say? The topic page Confluent hypergeometric functions lists several transformation formulas for the ${}_1F_1$ function. The relevant entries are dec042 which states $$\,{}_1F_1\!\left(-n, b, z\right) = \sum_{k=0}^{n} \frac{\left(-n\right)_{k}}{\left(b\right)_{k}} \frac{{z}^{k}}{k !}$$ subject to certain conditions on the variables, and be533c which states $$\,{}_1F_1\!\left(a, b, z\right) = {e}^{z} \,{}_1F_1\!\left(b - a, b, -z\right),$$ again subject to certain assumptions. After substitution and elementary simplifications, the first formula gives ${}_1F_1(-1,-1,1) = 2$ and the second formula gives ${}_1F_1(-1,-1,1) = e$. However, the parameters $(a,b,z) = (-1,-1,1)$ actually violate the assumptions stated in entry be533c, so only the first evaluation is valid, and there is no contradiction in Fungrim.

On the Wolfram Functions site, we find the formulas Hypergeometric1F1/03/01/04/02/0003 and Hypergeometric1F1/16/01/01/0001/ which contradict each other; note that full assumptions for the variables are not given.

A word of caution, however...

Strict mathematical consistency is nice as a goal, but implementing it in practice is not the easiest thing. The Fungrim formula language is still a work in progress, and many of the "globally-defined functions and constants with a fixed (and consistent) meaning" still only exist as such in my head. It will certainly be a lot of work to iron out all the special cases and write down the definitions. For example, the usual operators in calculus have ambiguities that needs to be resolved: directions of limits and derivatives, paths of integration, interpretation of improper integrals, and so on. Also, some formulas currently rely on implicit structural pattern matching which is not really well-defined and therefore needs to be replaced with more explicit semantic encoding in order to be unambiguously machine-readable.

Human error is also inevitable, but I plan to ensure a high level of reliability by implementing randomized testing. I don't plan to work on computer-aided formal proofs, and many entries in Fungrim are out of reach for current formal proof technology anyway, but if Fungrim is successful, perhaps other people will look at verifying some of the formulas in the future.

I should stress that Fungrim is intended to cover special functions and associated elements of real and complex analysis and number theory. It is emphatically not an attempt to cover all of mathematics. Fungrim is also not a research project into formalized foundations of mathematics, and common objects (like integers and real numbers) will just be taken for granted.

Graphics, tables and more

Graphics

I intend to populate Fungrim with publication-quality illustrations. This will include schematic diagrams, standard univariate function plots, and illustrations of complex functions using different visualization techniques. I only started working on this part a few days ago, so there are not many illustrations to show yet. So far, I've added a few "X-ray" plots of complex functions. I will quote the explanation given in Fungrim:

An X-ray plot illustrates the geometry of a complex analytic function $f\!\left(z\right)$. Thick black curves show where $\operatorname{Im}\!\left(f\!\left(z\right)\right) = 0$ (the function is pure real). Thick red curves show where $\operatorname{Re}\!\left(f\!\left(z\right)\right) = 0$ (the function is pure imaginary). Points where black and red curves intersect are zeros or poles. Magnitude level curves $\left|f\!\left(z\right)\right| = C$ are rendered as thin gray curves, with brighter shades corresponding to larger $|C|$. Blue lines show branch cuts. The value of the function is continuous with the branch cut on the side indicated with a solid line, and discontinuous on the side indicated with a dashed line. Yellow is used to highlight important regions.

As an example, the Modular j-invariant topic page features the following graphic:

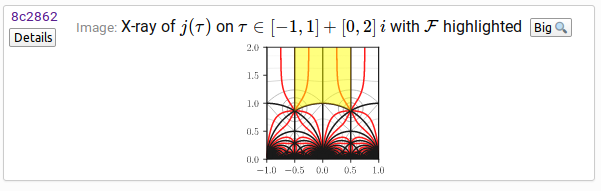
This small version is intended to be legible as-is, and it's in fact in SVG format so it looks great when zoomed in (not here in the screenshot, on the Fungrim page with the original SVG). Clicking the "Big" button results in a larger version:

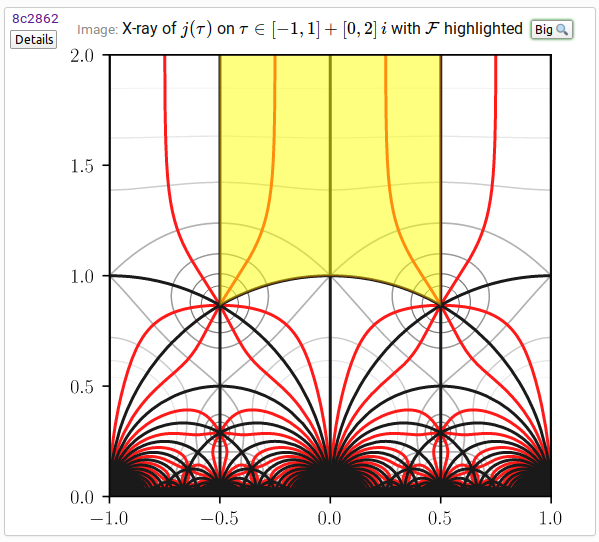
This is actually not just a magnification of the small version; it's a separate rendering with different font sizes and line widths. The difference is subtle but it matters! Everything is also designed with the lazy working scientist in mind: from the entry page for an image, you can you download PDF versions (ready to put into a LaTeX document with \includegraphics), SVG versions, and of course PNG versions in different resolutions.

Here is an X-ray for $\operatorname{atan}(z)$ featured on the Inverse tangent page, illustrating the branch cut locations:

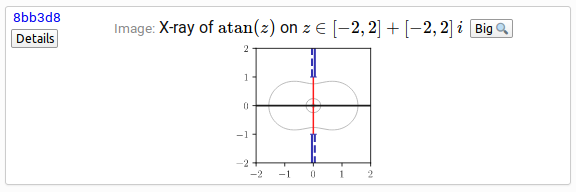
See the Gamma function, Riemann zeta function and Weierstrass elliptic functions for a few more neat examples!

All images added so far are generated using Python scripts included with the Fungrim source code, using Matplotlib for the actual rendering and a combination of mpmath and Python-FLINT for function evaluation.

Tables

No reference work on special functions would be complete without tables. Unlike graphics which are just decorative, tables include a semantic description of the data fields so that they can be read as theorems about the function values. Tables are currently just rendered to HTML, but I plan to add functionality to export tables to other formats. There is not much more to say, so I will just link to a few examples:

Proofs, references

At this time, I have no concrete plans to include proof information in Fungrim. I do try to include bibliographical references for "non-obvious" results that require non-elementary techniques to prove, especially when the origin cannot obviously be looked up in a place like Wikipedia or the DLMF. It would be nice if every entry had a reference to the literature or some kind of proof information, but I only have so much time!

What about the other reference works, then?

Indeed. I will quickly review some existing (online) reference works for special functions and point out the flaws that Fungrim attempts to address.

The DLMF

The NIST Digital Library of Mathematical Functions is a fantastic reference. It is extremely well edited, just as you would expect: the content is nicely structured, concise, and generally correct, with extensive bibliographical listings. The conciseness is also perhaps the biggest drawback: being the web companion of the NIST Handbook of Mathematical Functions, the scope of the DLMF was constrainted by page limits. A lot of (in my opinion) useful formulas are simply not covered, and others are stated as recipes ("for case X, the reader can combine Y with Z..."). The DLMF is especially lacking in its coverage of complex extensions and branch cuts for certain functions, and the coverage of inequalities is often lacking too.

Another drawback of the DLMF is that the content is not symbolic. The DLMF formulas use a special TeX encoding which is better than ordinary non-semantic TeX, but this representation is still not precise enough for symbolic computing. In addition, a lot of the information in the DLMF is presented as text and not in the formulas, and assumptions on variables are often implicit or incomplete.

Finally, the DLMF is unfortunately not open source, despite being a US government work. (It also goes offline whenever the US government shuts down, which seems to be a recurring event, but at least the paper version remains functional. Good old books.)

The Wolfram Functions Site

The Wolfram Functions Site is my favorite reference on special functions, and definitely a strong influence for Fungrim. All entries are generated from symbolic, semantic Mathematica source code which can be viewed on the website. The presentation can take some time to get used to, but for a power user, the Wolfram Functions Site is extremely handy. The coverage of special function identities is generally thorough, and the coverage of limiting cases and branch cuts is excellent apart from the occasional inconsistencies.

The drawbacks? Not open source, tied to the proprietary Mathematica language with its quirks, missing some categories of information (for example, the coverage of inequalities is often spotty). There are tens of thousands of ugly Mathematica-generated formulas that either express useless information or present useful information in an inelegant way. Many formulas include assumptions for the variables, but this is not always the case. The visual design of the website is a bit dated, but that's a very minor gripe.

Wikipedia, MathWorld, PlanetMath, etc.

There are many great online encyclopedias covering a broad range of mathematics including special functions, most importantly Wikipedia which is open source. Wikipedia is extensive to say the least, but also quite inconsistent. Some articles are perfectly structured and give you all the important information in the right order, others just state some half-wrong intuitions before they veer off into long trivia sections. The content is represented in a mixture of informal text and TeX; the mathematical data is not available in symbolic and semantic form. The definitions are rarely fully consistent between one article and the other. Illustrations are also inconsistent.

The DDMF

The Dynamic Dictionary of Mathematical Functions is an attempt to generate an encyclopedia of special functions semi-automatically. Each function is defined in terms of a differential equation, and all properties of the function are then derived algorithmically from first principles. This removes a lot of repeated human work (and potential for human error). The main drawback is the DDMF approach is that it is limited to D-finite functions and certain categories of formulas accessible by symbolic computation techniques. This paradigm covers a decent chunk of all special functions knowledge, but far from everything. The presentation in the DDMF also needs more work.

The LMFDB

The L-functions and Modular Forms Database is another fantastic project, but it has slightly different scope and goals. Fungrim will cover some aspects of L-functions and modular forms, but is not intended to be anywhere as in-depth in that domain.

OK, but what about computer algebra systems?

I think I have justified Fungrim as a "better reference work" at this point, but what about the second point I made at the top of this blog post: "the available computer algebra systems are not good enough"? This post is already so long that I think I will have to save a detailed writeup for another time, but you can get some hints from my slides.

Very briefly, computer algebra systems are full of bugs, and I think there are two main reasons for this:

Having made these observations, the connection to Fungrim is that many of the evaluation and simplification algorithms used for special functions and symbolic expressions could be represented by a minimal rewrite engine supported by a symbolic theorem database, instead of having ad-hoc code for every separate case. The Fungrim library could potentially be the database part of this solution. This motivates the focus on a semantic encoding for formulas, along with rigorous assumptions. The focus on rigorous symbolic assumptions is also a natural extension of my work with rigorous error bounds in Arb; indeed, one of my goals for the mathematical content in Fungrim is to have good coverage of inequalities with explicit constants suitable for use in rigorous numerical evaluation algorithms.

The idea of Fungrim-as-a-symbolic-library was inspired by Rubi, the rule-based symbolic integrator. Quoting from the website:

"[Rubi] uses pattern matching to uniquely determine which of its over 6600 integration rules to apply to a given integrand
Rubi dramatically out-performs other symbolic integrators, including Maple and Mathematica
Certainly much of analysis including equation solving, expression simplification, differentiation, summation, limits, etc. can be automated using this paradigm

Could Fungrim form the basis of a better symbolic engine for mathematical functions, similar to what Rubi has accomplished for the special case of symbolic integration? Right now, this is just a long-term possibility, and I don't have a concrete plan for developing such a library. I'm convinced that it can be done, but my immediate goal is just to make Fungrim useful as an ordinary reference work.

What are the development plans?

Right now, I'm mostly working on expanding the library of formulas in Fungrim. I still need to do some major work on the formula language, implement testing, etc. The code that generates the website is still a mess that needs a major cleanup. The README in the GitHub project lists some more TODO items for anyone who is interested. At this stage, I'm not exactly trying to recruit contributors to help out with the project, but code or content contributions are certainly welcome (especially if preceded by some discussion). Any feedback is also invited!



fredrikj.net  |  Blog index  |  RSS feed  |  Follow me on Mastodon  |  Become a sponsor