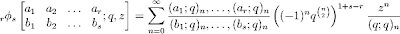Hypergeneralization

March 17, 2010

The generalized hypergeometric function can itself be generalized endlessly. I have recently implemented three such extensions in mpmath: bilateral series, two-dimensional hypergeometric series, and q-analog (or “basic”) hypergeometric series.

Bilateral series

The bilateral hypergeometric series is the simplest extension, and consists of taking the usual hypergeometric series and extending the range of summation from [0,∞) to (-∞,∞):

This series only converges when |z| = 1 and A = B, but interpreted as a sum of two ordinary hypergeometric series, it can be assigned a value for arbitrary z through the analytic continuation (or Borel regularization) of the ordinary hypergeometric series, which mpmath implements. Anyway, the convergent case is the interesting one. Here one obtains, for instance, Dougall's identityfor 2H2:

>>> from mpmath import *
>>> mp.dps = 25; mp.pretty = True
>>> a,b,c,d = 0.5, 1.5, 2.25, 3.25
>>> bihyper([a,b],[c,d],1)
-14.49118026212345786148847
>>> gammaprod([c,d,1-a,1-b,c+d-a-b-1],[c-a,d-a,c-b,d-b])
-14.49118026212345786148847

As an example of regularization, the divergent 1H0 series can be expressed as the sum of one 2F0 function and one 1F1 function:

>>> a = mpf(0.25)
>>> z = mpf(0.75)
>>> bihyper([a], [], z)
(0.2454393389657273841385582 + 0.2454393389657273841385582j)
>>> hyper([a,1],[],z) + (hyper([1],[1-a],-1/z)-1)
(0.2454393389657273841385582 + 0.2454393389657273841385582j)
>>> hyper([a,1],[],z) + hyper([1],[2-a],-1/z)/z/(a-1)
(0.2454393389657273841385582 + 0.2454393389657273841385582j)

Two-dimensional series

The most common hypergeometric series of two variables, i.e. a twodimensional series whose summand is a hypergeometric expression with respect to both indices separately, is the Appell F1 function, previously available in mpmath as appellf1:

However, much more general functions are possible. There are three other Appell functions: F2, F3, F4. The Horn functions are 34 distinct functions of order two, containing the Appell functions as special cases. The Kampé de Fériet function provides a generalization of Appell functions to arbitrary orders.

The new hyper2d function in mpmath can evaluate all these named functions, and more general functions still. The trick for speed is to write the series as a nested series, where the inner series is a generalized hypergeometric series that can be evaluated efficiently with hyper, and where the outer series has a rational recurrence formula. This rewriting also permits evaluating the analytic continuation with respect to the inner variable (as implemented by hyper).

The user specifies the format of the series in quasi-symbolic form, and the rewriting to nested form is done automatically by mpmath. For example, the Appell F1 function can be computed as

hyper2d({'m+n':[a], 'm':[b1], 'n':[b2]}, {'m+n':[c]}, x, y)

and indeed, this is essentially what appellf1 now does internally. The Appell F2-F4 functions have also been added explicitly as appellf2, appellf3, appellf4.

Hypergeometric functions of two (or more) variables have numerous applications, such as solving high-order algebraic equations, expressing various derivatives and integrals in closed form, and solving differential equations, but I have not yet found any simple examples that make good demonstrations except for F1. (I have mostly found examples of that take half a page to write down.) Any such examples for the documentation would be a welcome contribution!

Some trivial examples from the documentation are:

>>> x, y = mpf(0.25), mpf(0.5)
>>> hyper2d({'m':1,'n':1}, {}, x,y)
2.666666666666666666666667
>>> 1/(1-x)/(1-y)
2.666666666666666666666667
>>> hyper2d({'m':[1,2],'n':[3,4]}, {'m':[5],'n':[6]}, x,y)
4.164358531238938319669856
>>> hyp2f1(1,2,5,x)*hyp2f1(3,4,6,y)
4.164358531238938319669856
>>> hyper2d({'m':1,'n':1},{'m+n':1},x,y)
2.013417124712514809623881
>>> (exp(x)*x-exp(y)*y)/(x-y)
2.013417124712514809623881

An example of a Horn function, H3:

>>> x, y = 0.0625, 0.125
>>> a,b,c = 0.5,0.75,0.625
>>> hyper2d({'2m+n':a,'n':b},{'m+n':c},x,y)
1.190003093972956004227425
>>> nsum(lambda m,n: rf(a,2*m+n)*rf(b,n)/rf(c,m+n)*\
...     x**m*y**n/fac(m)/fac(n), [0,inf], [0,inf])
1.190003093972956004227425

This also demonstrates the recently added generic support for multidimensional infinite series in mpmath. But of course, nsum is much slower than hyper2d.

Hypergeometric q-series

Before introducing the q-analog of the hypergeometric series, I should introduce the q-Pochhammer symbol,

This itself is a new function in mpmath, implemented as qp(a,q,n) (with two- and one-argument forms qp(a,q) and qp(q) also permitted) and is the basis for more general computation involving q-analogs. The q-factorial and q-gamma function have also been added (as qfac and qgamma), but are not yet documented.

The q-analogs have important applications in number theory. As a very neat example, numerically computing the Taylor series of 1/(q, q)_∞with mpmath gives

>>> taylor(lambda q: 1/qp(q), 0, 10)
[1.0, 1.0, 2.0, 3.0, 5.0, 7.0, 11.0, 15.0, 22.0, 30.0, 42.0]

These are the values of the partition function P(n) for n = 0,1,2,..., i.e. the number of ways of writing n as a sum of positive integers.

Replacing the rising factorials (Pochhammer symbols) in the generalized hypergeometric series with their q-analogs gives the hypergeometric q-series or basic hypergeometric series

This function is implemented as qhyper. Like hyper, it supports arbitrary combinations of real and complex arguments (assuming |q| < 1). Some examples from the documentation:

>>> qhyper([0.5], [2.25], 0.25, 4)
-0.1975849091263356009534385
>>> qhyper([0.5], [2.25], 0.25-0.25j, 4)
(2.806330244925716649839237 + 3.568997623337943121769938j)
>>> qhyper([1+j], [2,3+0.5j], 0.25, 3+4j)
(9.112885171773400017270226 - 1.272756997166375050700388j)

Like hyper, it automatically ensures accurate evaluation for alternating series:

>>> q = 0.998046875
>>> mp.dps=5; qhyper([2],[0.5], q, -0.5)
6.6738e-69
>>> mp.dps=15; qhyper([2],[0.5], q, -0.5)
6.67376764851253e-69
>>> mp.dps=25; qhyper([2],[0.5], q, -0.5)
6.673767648512527695718826e-69
>>> mp.dps=100; qhyper([2],[0.5], q, -0.5)
6.673767648512527695718826106778799352769798151218768443717704076836963752188876561888441662933081804e-69

With the q-analog of the generalized hypergeometric function implemented, it becomes possible to compute q-exponentials, q-sines, q-orthogonal polynomials, q-Bessel functions, and pretty much anything else. If there is interest, such function could be added explicitly to mpmath.

For more information and examples of the functions discussed in this post, see the sections on hypergeometric functions and q-functions (a little terse at the moment) in the mpmath documentation.

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor