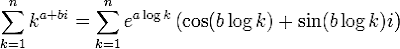Speedups of elementary functions

March 11, 2010

I have a fairly large backlog of changes in mpmath to blog about. For today, I’ll just briefly mention the most recent one, which is a set of optimizations to elementary functions. The commit is here. I intend to provide much faster Cython versions of the elementary functions some time in the future, but since there was room for optimizing the Python versions, I decided to invest a little time in that.

Most importantly, the asymptotic performance of trigonometric function has been improved greatly, due to a more optimized complexity reduction strategy. The faster strategy was previously used only for exp, but cos/sin are virtually identical in theory so fixing this was mostly a coding problem. In fact, the high-precision code for exp/cosh/sinh/cos/sin is largely shared now, which is nice because only one implementation needs to be optimized.

The following image shows performance for computing cos(3.7). The red graph is the old implementation; blue is new. The top subplot shows evaluations/second at low precision, i.e. higher is better, and the bottom subplot shows seconds/evaluation at higher precision, i.e. lower is better.

Already at a few thousand bits, the new code is more than twice as fast, and then it just gets better and better. There is also a little less overhead at low precision now, so the new code is uniformly faster.

Also exp, cosh and sinh have been optimized slightly. Most importantly, there is a little less overhead at low precision, but asymptotic speed has also improved a bit.

Performance for computing cosh(3.7):

Performance for computing exp(3.7):

I should note that the performance depends on some tuning parameters which naturally are system-specific. The results above are on a 32-bit system with gmpy as the backend. I hope to later implement optimized tuning parameters for other systems as well.

Elementary function performance is of course important globally, but it’s especially important for some specific functions. For example, the speed of the Riemann zeta function depends almost proportionally on the total speed of evaluating one exp, one log, one sine, and one cosine, since the main part of the work consists of summing the truncated L-series

With the improved elementary functions, and some overhead removals to the zetasum code in the same commit, the Riemann zeta function is up to 2x faster now, and about 50% faster on the critical line.

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor