Accelerated arithmetic in Arb 2.15

September 18, 2018

I have just issued version 2.15 of Arb. As usual, downloads are available via GitHub.

The big news in Arb 2.15 is that polynomial and matrix arithmetic is significantly faster in the basecase regimes. The speedup is typically about 2x for polynomials and matrices of size 10 to 30 when the precision is 1-2 words (up to 128 bits), with varying levels of improvement in other ranges. For certain operations, more than a 4x speedup is possible. The improvement is due to use of fast dot product evaluation in combination with more accurate cutoffs between different algorithms.

Arb 2.15 adds the functions arb_dot and acb_dot for computing dot products $\sum_{k=1}^N a_k b_k$. The normal way to compute a dot product until now was to do fused multiply-adds with arb_addmul / acb_addmul in a loop. However, each such multiply-add has to produce fully normalized arb_t or acb_t output. The main idea behind the new dot product functions is to treat the whole dot product as an atomic operation and avoid normalization and bookkeeping overhead for each partial sum. In addition to this, the new dot product functions inspect the error bounds for all entries in the vectors and for each term $a_k b_k$ only compute the leading bits that actually contribute to the final result, saving even more time when the terms vary in magnitude or have large radii.

There are also new functions arb_approx_dot and acb_approx_dot which compute floating-point dot products without error bounds, useful for approximate linear algebra.

The following table compares the performance of four methods to compute a dot product of two length-N vectors of real numbers (here, all numbers have roughly the same magnitude).

mpfr_dot is a simple MPFR implementation calling mpfr_mul and mpfr_add in a loop (MPFR has a fused multiply-add function, but it is actually slower)
arb_dot_simple is a simple Arb implementation calling arb_addmul in a loop
arb_dot is the new, optimized dot product
arb_approx_dot is the new, optimized dot product without error bounds

The table shows timings in nanoseconds (lower is better).

N	prec	mpfr_dot	arb_dot_simple	arb_dot	arb_approx_dot
10	64	300	710	217	109
10	128	900	840	295	177
10	256	1240	1150	660	560
10	1024	3600	3400	2780	2700
10	4096	21300	24800	21300	21100
10	16384	173000	202000	172000	172000
100	64	3200	7700	1760	830
100	128	9300	8800	2320	1470
100	256	12700	12200	6000	5100
100	1024	35000	35000	26600	26000
100	4096	218000	256000	210000	211000
100	16384	1760000	2070000	1730000	1720000

At low precision, the new dot product functions are not only several times faster than the simple algorithm using arb_addmul; they are even significantly faster than MPFR arithmetic! Under ideal conditions, arb_dot reaches an equivalent performance of more than 100 million ball operations per second (where one ball addition or multiplication counts as an operation) while arb_approx_dot reaches more than 200 million floating-point operations per second. (This is on a 1.9 GHz Intel i5-4300U CPU.)

Complex numbers are uniformly about four times more expensive than real numbers:

N	prec	acb_dot_simple	acb_dot	acb_approx_dot
10	64	3000	850	420
10	128	3600	1070	690
10	256	5700	2920	2560
10	1024	15100	11400	10600
10	4096	96000	85000	85000
10	16384	660000	660000	660000

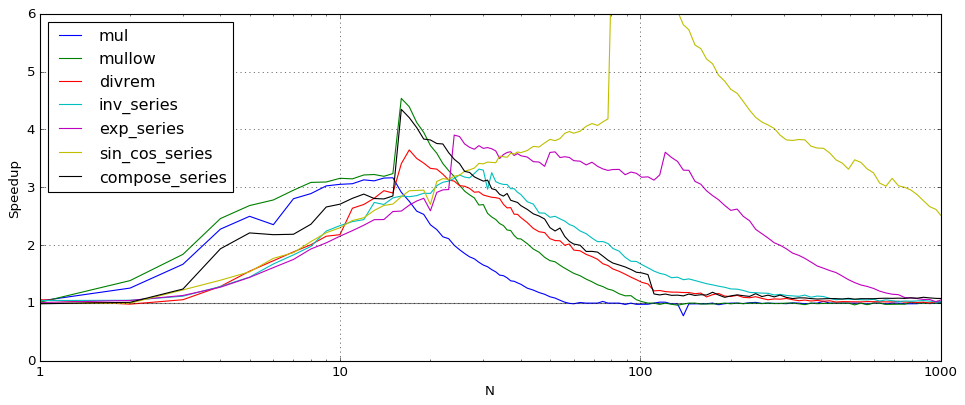
In Arb 2.15, calls to the new arb_dot and acb_dot functions have replaced the inner loops in basecase polynomial multiplication, matrix multiplication, power series inversion, triangular solving and many other operations. The following plot shows the speedup between Arb 2.14 and Arb 2.15 for various polynomial and power series operations, where N is the polynomial or series length. The comparison here is for complex arithmetic (acb_poly) at 64-bit precision.

The following plot shows the speedup for matrix operations, where the matrices have size N. The comparison here is likewise for complex arithmetic (acb_mat) at 64-bit precision.

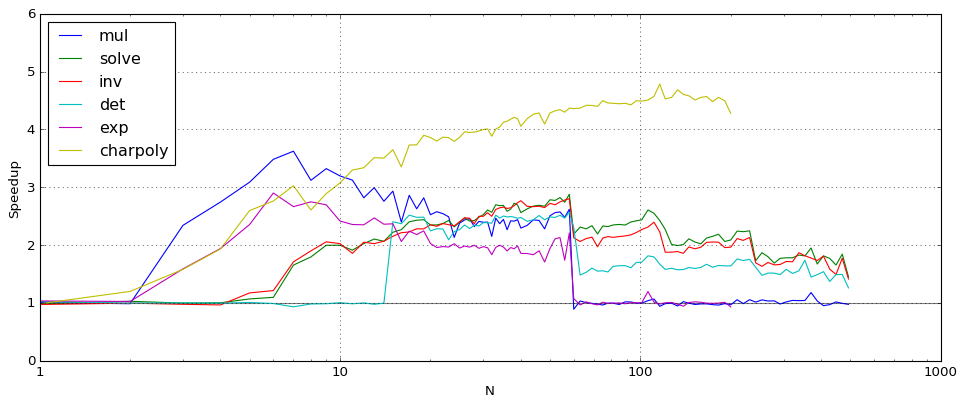
When N is large enough, the new dot product code gives no improvement for most operations since Arb tries to reduce everything asymptotically to multiplying huge polynomials or matrices via FLINT. One visible exception is charpoly which currently does not use a reduction to matrix multiplication, so the pure dot product speedup is exhibited.

I would be interested in reports from users about whether the improvements are visible in "real-world" applications!

The dot product code was a lot of work to design and implement. In fact, I started working on it in spare evenings during my summer vacation in August so that I could take the time to meditate on the problem and figure it out slowly without other work-related distractions. I have not had time to work on any other major features in time for this release, but a small new feature in Arb 2.15 worth pointing out is a function for computing Airy function zeros (arb_hypgeom_airy_zero). Having this function in the library mostly serves the purpose of "special functions table-filling", but it will hopefully be useful to someone at some point!

fredrikj.net | Blog index | RSS feed | Follow me on Mastodon | Become a sponsor