fredrikj.net / blog /

What's new in FLINT 3.1

February 25, 2024

We have just released FLINT 3.1. Thanks to all contributors, and especially to Albin Ahlbäck who has been extremely active. Indeed, Albin is now officially a co-maintainer of FLINT.

I should apologize for not having done a writeup for FLINT 3.0 last year. The list of changes was simply too daunting! The 3.1 release is a much smaller one, but there are still lots of nice things to highlight. See the history page for items that have been omitted in this blog post.

Contents

Riemann theta function

A major new feature in FLINT 3.1 is the Riemann theta function $\theta_{a,b}(z, \tau)$, a multidimensional generalization of the classical Jacobi theta functions with various scientific applications.

This important special function of several complex variables has finally been implemented in full generality by Jean Kieffer, using a new quasilinear algorithm developed by Kieffer and Noam Elkies which will be described in a forthcoming paper. Besides the theta function itself, it is possible to evaluate derivatives to any order to arbitrary precision with rigorous error bounds. There are also functions to evaluate Siegel modular forms which can be expressed in terms of $\theta_{a,b}(z, \tau)$ in the dimension $g = 2$ case.

The very impressive (and well-documented) implementation comprises more than 12,000 lines of code including tests for the new acb_theta module alone. In addition to this, Jean Kieffer has contributed many other helper functions for working with complex vectors and with symmetric positive-definite matrices which are used behind the scenes.

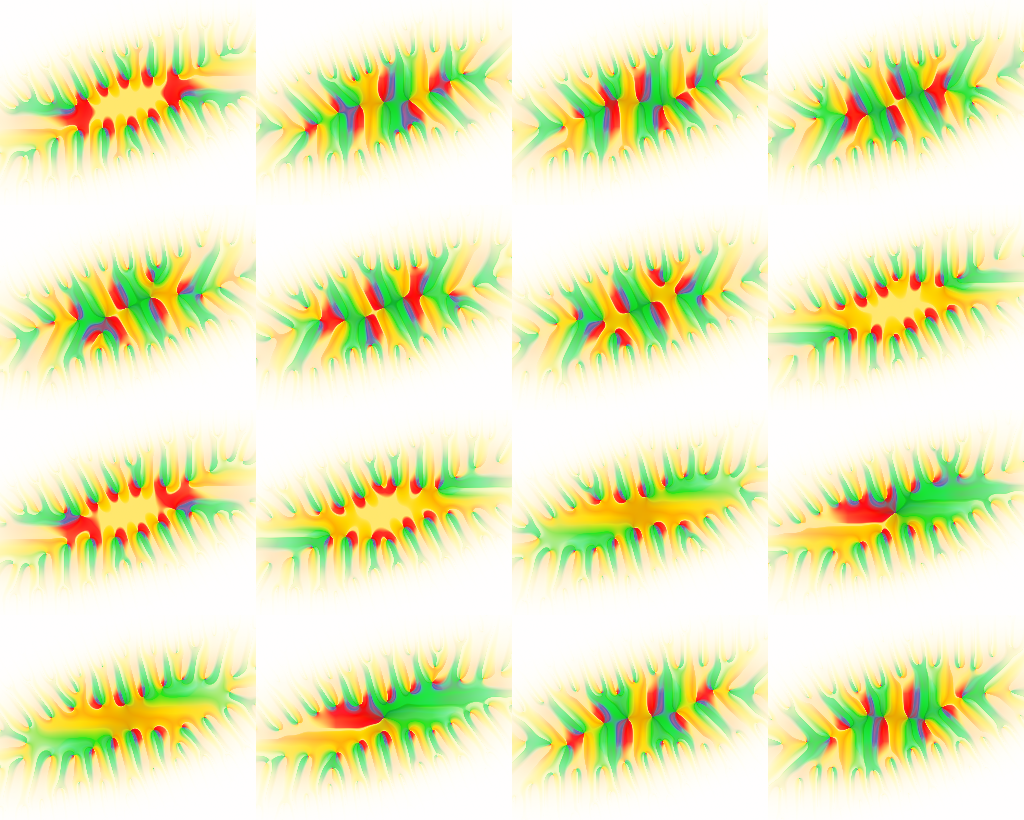
Montage: plots of the Riemann theta function $\theta_{a,b}([z, -iz/2], \tau)$ with period matrix $\tau = \small \begin{pmatrix} 1+2i & -1-i \\ -1-i & 1+2i \end{pmatrix}$ for all 16 pairs of characteristics $(a,b)$ in dimension $g = 2$.

At extremely high precision, the Riemann theta function is actually faster than the classical Jacobi theta functions in FLINT, as the latter currently do not use a quasilinear algorithm. For example, computing $\theta_3(0.75+0.625i, i)$ to 100,000 digits currently takes 1.26 seconds with the classical Jacobi theta function implementation and 0.23 seconds via the new Riemann theta function code. In a future version, we will improve the classical Jacobi theta functions and $\mathsf{SL}(2,\mathbb{Z})$ modular forms to use the Riemann theta function internally when this is more efficient.

Benchmarking

FLINT 3.1 is the first version to include an official benchmark suite intended to allow tracking aggregate performance changes. Compared to FLINT 3.0, there is an overall 15% speedup on my machine:

                                      FLINT 3.0   FLINT 3.1
==================== BY GROUP ==============================
fmpz (18 benchmarks)                     19.310      14.848
fmpz_poly (17 benchmarks)                15.340      12.291
nmod_mpoly (8 benchmarks)                11.411      11.253
fmpz_mpoly (2 benchmarks)                 1.502       1.487
arb (11 benchmarks)                      13.232      12.580
calcium (1 benchmarks)                    3.633       2.138
====================== TOTAL ===============================
all (57 benchmarks)                      64.428      54.597

The speedup is due to several small optimizations, some of which will be recounted below (others can be found in the changelog). Do take this figure with a grain of salt: the current collection of benchmarks covers certain functionality including polynomial factorisation and Arb-based numerical computation while neglecting other important parts of the library such as finite field arithmetic and exact linear algebra. Some applications will run faster with FLINT 3.1; others will not be affected. One of the goals for FLINT 3.2 will be to develop a more comprehensive benchmark suite.

New basecase integer multiplication

FLINT 3.1 has new basecase integer multiplication code which performs better than GMP. There is both generic C code (giving a small speedup for short operands on non-x86-64 machines) and dedicated assembly code for recent x86-64 CPUs (giving a significant speedup for a much larger range of operands). The assembly code is the work of Albin Ahlbäck.

On my machine (Zen3), I get a 2.4x speedup over GMP 6.3's mpn_mul_n for a 3x3 limb multiply, 1.5x speedup for 8x8 limbs, and a 1.1x speedup for 32x32 limbs:

To benefit, users can simply call flint_mpn_mul_n, flint_mpn_mul or flint_mpn_sqr instead of their GMP counterparts. The flint_mpn_* functions were already faster than GMP for huge operands due to our small-prime FFT, but now they make sense for small operands too.

These functions are used internally by FLINT and thus speed up a lot of other functions indirectly. However, high-level workloads will typically see a smaller speedup since functions like fmpz_mul have a lot of overhead; to benefit maximally, one needs to work with mpn operands directly. We will optimize future versions of FLINT to take better advantage of these new arithmetic primitives.

How did we manage to get a speedup over GMP, which is quite well optimized for small operands? In short, instead of having a single basecase multiplication routine (GMP's mpn_mul_basecase), we generate an optimized $n \times m$ kernel for each small pair $n$ and $m$ (currently up to $16 \times 8$). Larger multiplications are then reduced to blockwise products. The fixed-length kernels can do everything in registers, have no loop overhead, and the case dispatch can be done efficiently using a function pointer table lookup.

There is also assembly code for truncated multiplication (mulhigh), which will benefit numerical algorithms, but this code is currently unused and will be fully integrated in a future version.

Note that there is a potential drawback to the new multiplication code: having many different basecase kernels results in much larger code size than GMP, and some applications might actually slow down due to instruction cache misses. Number-crunching-heavy applications should benefit, however.

Faster and smaller builds

The effort to debloat FLINT and streamline development continues:

This is despite a ton of new features. As noted above, the Riemann theta function alone accounts for more than 12,000 added lines of code; assembly multiplication routines account for another 10,000 added lines.

Much of the binary size reduction comes from removing -funroll-loops as a default compiler flag; loop unrolling is now applied much more selectively. Another notable size reduction comes from compressing the database of Conway polynomials by 90%, saving roughly 1 MB. Several thousand lines of code have been removed manually by replacing various duplicated algorithm implementations with generics wrappers.

Most of the test suite compilation speedup comes from merged compilation. To improve the time running the tests, we have tweaked the number of iterations for some slow-running tests while adding more targeted tests to increase the overall test coverage.

Nicer test printing

Also worth mentioning is that the output from make -j check is much nicer now. Previously, we got scrambled content: 

$ make -j check MOD=fmpz_mpoly_q
add....add_fmpq....add_fmpz....div....div_fmpq....div_fmpz....inv....mul....PASS
mul_fmpq....mul_fmpz....randtest....sub....sub_fmpq....PASS
sub_fmpz....PASS
PASS
PASS
PASS
PASS
PASS
PASS
PASS
PASS
PASS
PASS
PASS

Now, the full function name is printed and then re-printed with the PASS (or FAIL) statement, and we get a timing result for each test:

fredrik@mordor:~/src/flint$ make -j check MOD=fmpz_mpoly_q
fmpz_mpoly_q_add...
fmpz_mpoly_q_add_fmpz...
fmpz_mpoly_q_div_fmpq...
fmpz_mpoly_q_get_set_str...
fmpz_mpoly_q_mul...
fmpz_mpoly_q_mul_fmpz...
fmpz_mpoly_q_sub...
fmpz_mpoly_q_sub_fmpz...
fmpz_mpoly_q_get_set_str                          0.00   (PASS)
fmpz_mpoly_q_inv...
fmpz_mpoly_q_inv                                  0.00   (PASS)
fmpz_mpoly_q_add_fmpz                             0.00   (PASS)
fmpz_mpoly_q_div...
fmpz_mpoly_q_sub_fmpz                             0.00   (PASS)
fmpz_mpoly_q_div_fmpq                             0.01   (PASS)
fmpz_mpoly_q_div_fmpz...
fmpz_mpoly_q_mul_fmpz                             0.00   (PASS)
fmpz_mpoly_q_randtest...
fmpz_mpoly_q_randtest                             0.00   (PASS)
fmpz_mpoly_q_div_fmpz                             0.01   (PASS)
fmpz_mpoly_q_mul                                  0.02   (PASS)
fmpz_mpoly_q_mul_fmpq...
fmpz_mpoly_q_mul_fmpq                             0.00   (PASS)
fmpz_mpoly_q_div                                  0.02   (PASS)
fmpz_mpoly_q_add                                  0.07   (PASS)
fmpz_mpoly_q_add_fmpq...
fmpz_mpoly_q_add_fmpq                             0.00   (PASS)
fmpz_mpoly_q_sub                                  0.10   (PASS)
fmpz_mpoly_q_sub_fmpq...
fmpz_mpoly_q_sub_fmpq                             0.00   (PASS)

All tests passed for fmpz_mpoly_q.

Exact polynomial division

FLINT 3.1 adds the functions fmpz_poly_divexact and nmod_poly_divexact for computing exact polynomial quotients $h = f / g$. This is useful, for example, in fraction-free matrix algorithms and when removing GCDs in rational function arithmetic. The divexact methods are significantly faster than the truncating counterparts fmpz_poly_div and nmod_poly_div for typical operands; see some tables here and here.

Faster formulas for mathematical constants

FLINT 3.1 uses recently discovered hypergeometric series by Jorge Zuniga and Jesús Guillera to compute some fundamental mathematical constants: $\log(2)$, Catalan’s constant, $\zeta(3)$ and $\Gamma(1/3)$. For $\log(2)$ the new formula is twice as fast. FLINT 3.0:

$ build/examples/pi 10000000 -constant log2
precision = 33219285 bits... cpu/wall(s): 8.557 8.557
virt/peak/res/peak(MB): 115.13 162.44 99.98 147.20
[0.69314718055994530941{...9999960 digits...}80135652602465385883 +/- 3.19e-10000001]

FLINT 3.1:

$ build/examples/pi 10000000 -constant log2
precision = 33219285 bits... cpu/wall(s): 4.084 4.084
virt/peak/res/peak(MB): 156.73 156.73 145.55 145.55
[0.69314718055994530941{...9999960 digits...}80135652602465385883 +/- 3.19e-10000001]

FLINT 3.1 also adds the reciprocal Fibonacci constant.

Integer dot products and matrix multiplication

Dot products of fmpz and fmpz_mod vectors are now implemented using efficient mpn-level code rather than naive fmpz_addmul loops, and these more efficient dot products are now used in various fmpz_poly, fmpz_mod_poly, fmpz_mat and fmpz_mod_mat basecase algorithms. Further, fmpz_mat_mul has been optimized in certain ranges by using Waksman multiplication instead of Strassen's algorithm (contributed by Éric Schost, Vincent Neiger), and fmpz_mat_sqr has been optimized for small matrices (contributed by Marco Bodrato) and in general through better algorithm selection.

As a result, various operations on matrices and polynomials over $\mathbb{Z}$ or $\mathbb{Z}/n\mathbb{Z}$ should be faster for certain ranges of input. Here is just one data point: solving a 50x50 linear system over $\mathbb{Z}/n\mathbb{Z}$ with a 1000-digit modulus $n$ takes 0.178 seconds with FLINT 3.0 and 0.133 seconds with FLINT 3.1 (a 1.34x speedup).

Related to this, the fmpz_mod_mat module has been redesigned to use a context object, improving performance and making the interface consistent with other modules. There is also finally an fmpz_mod_mat_det method.

Faster univariate factorization

Factoring in $\mathbb{Z}[x]$ is faster in FLINT 3.1: on our collection of 17 hard benchmark polynomials, the overall speedup is 1.25x, with some polynomials factoring more than 1.5x faster. The faster polynomial factorization also results in faster qqbar arithmetic.

Some of the improvement is due to faster polynomial arithmetic, but most is actually due to fixing some easy bottlenecks (expensive conversions and ldexp calls) in the floating-point code for computing CLD bounds.

Expression parsing, printing

The method gr_set_str now supports parsing arbitrary arithmetical expressions, over any ring. One of the uses is to construct numerical constants from decimal literals or symbolic formulas (here illustrated with interactive examples using flint_ctypes):

>>> QQ("2 / 3")
2/3

>>> QQ("2^10 / 3 + 1")
1027/3

>>> RR("1.23e-4")
[0.0001230000000000000 +/- 4.61e-20]

>>> QQ("1.23e-4")
123/1000000

>>> QQbar("0.2 + 3.1e-4*i")
Root a = 0.200000 + 0.000310000*I of 10000000000*a^2-4000000000*a+400000961

>>> QQbar("(-1/2*i)^(1/3)")
Root a = 0.687365 - 0.396850*I of 4*a^6+1

>>> CC("(-1/2*i)^(1/3)")
([0.687364818499301 +/- 6.67e-16] + [-0.396850262992050 +/- 5.78e-16]*I)

The parser code recognizes the generators in recursively defined structures, illustrated here for a multivariate polynomial ring with number field coefficients $R = (\mathbb{Q}(a) / \langle a^2+1 \rangle)[x,y]$:

>>> R = PolynomialRing_gr_mpoly(NumberField(ZZx.gen()**2+1, "a"), 2, ["x", "y"])
>>> R("(a+x+2*y)^2")
x^2 + 4*x*y + (2*a)*x + 4*y^2 + (4*a)*y - 1
>>> R(str(R("(a+x+2*y)^2")))
x^2 + 4*x*y + (2*a)*x + 4*y^2 + (4*a)*y - 1

In effect, most rings now support roundtripping: pretty-printed output from gr_get_str can be parsed back with gr_set_str. (There are still some exceptions, which will be implemented in a future version.)

For rings based on ball arithmetic, we can parse error bounds expressed using the $\pm$ operator. We can even mix exact symbols like $\pi$ and decimal literals this way: 

>>> RR("pi +/- 1e-6")
[3.14159 +/- 3.66e-6]

>>> RR("(pi +/- 1e-10) +/- 1e-5")
[3.1416 +/- 1.74e-5]

>>> CC("(1+i) +/- (1e-5 + 1e-7*i)")
([1.0000 +/- 1.01e-5] + [1.000000 +/- 1.01e-7]*I)

A further neat example: we can parse elements of $\mathbb{R}[x]$ with coefficientwise error bounds. In fact, the error term can be a polynomial of radii.

>>> RRx("[1/3 +/- 1e-10]*x + (-0.35 +/- 1e-12)*x^2")
[0.333333333 +/- 4.34e-10]*x + [-0.35000000000 +/- 1.01e-12]*x^2

>>> RRx("(1 + x + x^2) +/- (0.003 + 0.004*x + 0.005*x^2 + 0.006*x^3)")
[1.00 +/- 3.01e-3] + [1.00 +/- 4.01e-3]*x + [1.00 +/- 5.01e-3]*x^2 + [+/- 6.01e-3]*x^3

A related nice quality-of-life improvement is that flint_printf and friends now support printing many FLINT types. For example, one can write flint_printf("%{fmpz} / %{fmpz} = %{fmpq}\n", a, b, c); where a, b are fmpz_t's and c is an fmpq_t. Previously, this would have required a sequence of calls to printf, fmpz_print and fmpq_print.

Configuration improvements

The default optimization flags have been changed to -O3 -march=native (previously -O2 -funroll-loops). In general, this should result in faster code. A notable consequence is that the small-prime FFT will be enabled by default on supported machines, and many more functions should now use vector instructions.

Using -O3 does not always result in faster code than -O2: we have found a few critical functions where this caused a slowdown with GCC, and added workarounds.

We have fixed various other issues affecting performance: for example, the correct assembly routines are now used when compiling with GCC on ARM64, and the thresholds for using fft_small have been adjusted for underperforming (i.e. Intel) CPUs.

License change

FLINT's license has been changed from "LGPL 2.1 or later" to "LGPL 3 or later". This was mainly done in order to be able to use modified code from other LGPL 3-licensed libraries like GMP and MPFR.



fredrikj.net  |  Blog index  |  RSS feed  |  Follow me on Mastodon  |  Become a sponsor