fredrikj.net / blog /

Arb 2.12 released

November 29, 2017

I have finally tagged version 2.12.0 of Arb. There are many major new features: code for numerical integration, code for DFTs of complex vectors (contributed by Pascal Molin), fast evaluation of Legendre polynomials, performance optimizations for elementary functions, improvements to elliptic functions, and a few important bugfixes. A full changelog is included at the end of this post.

Numerical integration

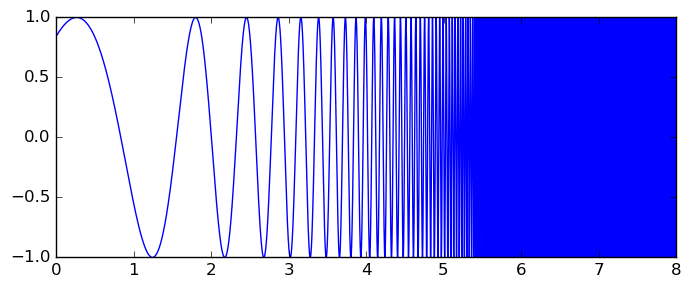
As discussed in depth in the most recent post, Arb now includes fast, robust and easy-to-use code for computing integrals with rigorous error bounds. A nice example is Rump's oscillatory integral $\int_0^8 \sin(x + e^x) dx$ (integrand pictured below), which Arb evaluates to 1000-digit accuracy in 1.2 seconds.

Discrete Fourier transforms

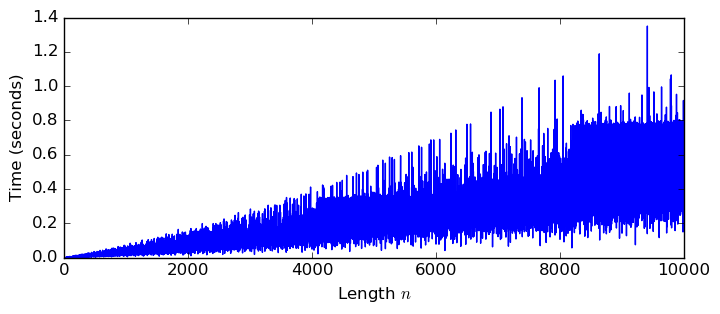
Pascal Molin contributed the acb_dft module covering computation of discrete Fourier transforms (DFTs) of complex vectors. As usual, power-of-two lengths $n = 2^k$ are the most efficient, but different FFT algorithms have been implemented to ensure that the complexity is $O(n \log n)$ even for $n$ with large prime factors. The plot shows the time to compute a length-$n$ DFT with 100-digit precision.

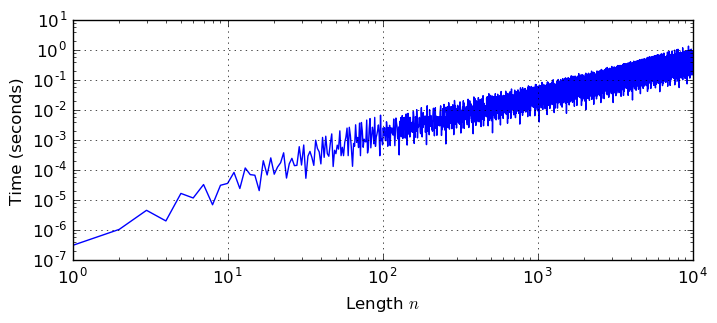
With a logarithmic scale:

There are many possible uses for DFTs, including interpolation, multipoint evaluation, and polynomial multiplication (the normal polynomial multiplication code in Arb which relies on FLINT is superior for single multiplications, but DFTs can be recycled to speed up multiplications when the same operands are used several times).

An application of DFTs in number theory is fast multi-evaluation of Dirichlet L-functions $L(s,\chi)$ for fixed $s$ over the whole group of characters $\chi$ of a given modulus $q$. The program examples/lcentral.c checks that $L(1/2,\chi)$ is nonzero for all characters $\chi$ for all $q$ in a given range. Here we run it with 128-bit precision and $q = 10^6$, which takes 9.1 seconds, where slightly more than half the time is spent computing a DFT of length $\phi(10^6) = 4 \cdot 10^5$: 

build/examples/lcentral --prec 128 --check --quiet 1000000 1000000
cpu/wall(s): 9.079 9.073
virt/peak/res/peak(MB): 93.68 203.84 69.74 179.72

The current FFT code just uses straight acb_t arithmetic, so it has a lot of overhead for each arithmetic operation at low precision. With 53-bit precision, it is more than 100 times slower than an optimized double FFT library. Significant future optimization in this area is possible.

Fast and accurate evaluation of Legendre polynomials

New code has been added for evaluating Legendre polynomials $P_n(x)$ for real $-1 \le x \le 1$ and word-size integer $n$. This code is much faster than the generic complex code used previously and gives accurate enclosures for large $n$ without requiring $O(n)$ extra precision. The improvement is significant even for moderate $n$: for example, $P_{100}([0.3 \pm 10^{-15}])$ previously took 36 microseconds and returned [0.06 +/- 4.46e-3]. It now takes 13 microseconds and returns [0.057127392203 +/- 3.44e-13]. The same $x$ with $n = 10^6$ takes 23 microseconds and returns [-0.00054506 +/- 3.16e-9] (with the old code, million-bit precision would have been needed). This is a plot of $P_{10^N+1}(x)$ for $N = 1,2,3,4,5,6$, generated at 53-bit precision:

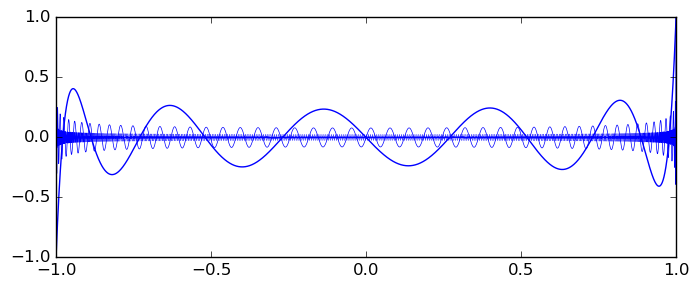
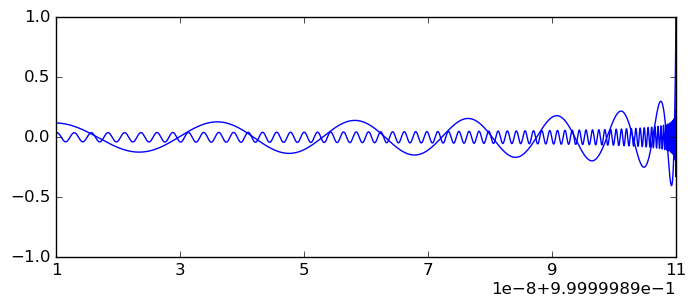
Detail of $P_{10^5+1}(x)$ and $P_{10^6+1}(x)$ on $[0.9999999,1]$:

There is also a new function for computing the roots of Legendre polynomials and the associated Gauss-Legendre quadrature weights (which gets called internally by the new integration code). Generating the set of roots and quadrature weights with $n = 1000$ takes 0.07 seconds at 64-bit precision and 1.3 seconds at 1000-digit precision. The degree-10000 roots and weights with 10000-digit precision take 700 seconds. At any fixed precision, the time per node is $O(1)$ when $n \to \infty$. For example, with 1000-digit precision, the whole set with $n = 10^5$ takes 221 seconds while $n = 10^6$ at the same precision takes 2016 seconds.

The new code for Legendre polynomials was developed in collaboration with Marc Mezzarobba and will be described in a forthcoming paper.

Faster high-precision elementary functions

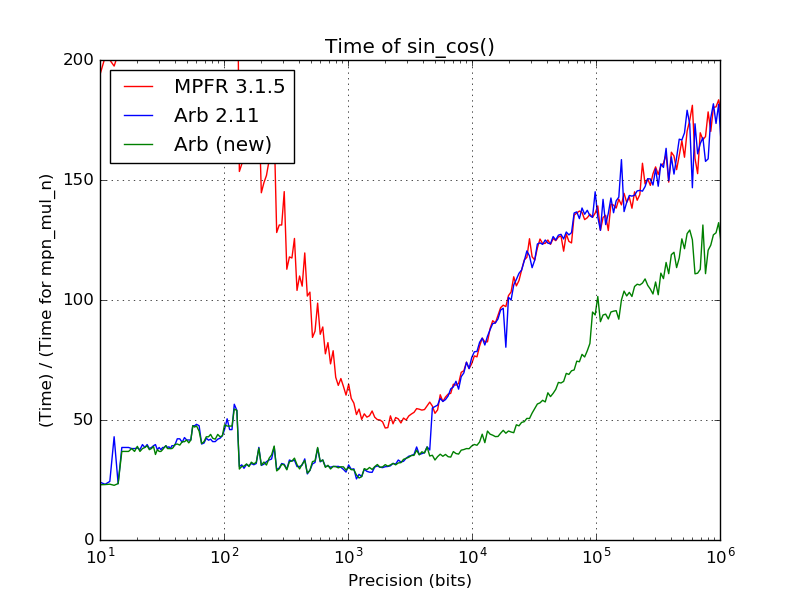
This was already covered in a previous post, so I just repeat the main results here. At high precision, the sine and cosine functions are now computed using custom binary splitting code instead of calling MPFR. This is up to twice as fast (near 10000 digits) and 30-40% faster asymptotically. The exponential function has also been optimized in the range from about 1400 to 6000 digits.

Improved elliptic functions

Several improvements have been made to elliptic and related functions:

In related news, my slides on "Numerics of classical elliptic functions, elliptic integrals and modular forms" from a workshop at DESY in October contain some more information about the algorithms for elliptic functions.

Full changelog



fredrikj.net  |  Blog index  |  RSS feed  |  Follow me on Mastodon  |  Become a sponsor